Rotation Matrix and SO(3) Groups

Introduction

In the previous post, we derive a formal definition of rigid body motion (or transformation). Here, we show that rotational motion of rigid object in 3D space is one of the rigid body transformations.

Definition of Rotation Matrix

Consider a rigid object fixed at point \(O\) (Figure 1). The rigid object can freely rotate about point \(O\), and our goal is deriving a mathematical expression to describe its rotational motion.

To describe the rotational motion of a rigid object, we consider two frames: a fixed, inertial frame \(\{S\}\) (Figure 1, Left) and a body-fixed frame \(\{B\}\) attached to the body (Figure 1, Right). The rotational motion of the rigid object can be studied by analyzing the relative orientation between two frames, \(\{S\}\) and \(\{B\}\).

We define the rotation matrix \({}^s\mathbf{R}_b\), which represents the coordinates of the basis of frame \(\{B\}\) with respect to frame \(\{S\}\). In detail, let the frame \(\{B\}\) and \(\{S\}\) consist of three basis vectors \(\hat{e}_1,\hat{e}_2,\hat{e}_3\) and \(\hat{e}_X,\hat{e}_Y,\hat{e}_Z\), respectively. The basis vectors of frame \(\{B\}\) can be expressed with the basis vectors of frame \(\{S\}\): \[ \begin{align} \hat{e}_1 &= r_{11} \hat{e}_X + r_{21} \hat{e}_Y + r_{31}\hat{e}_Z \\ \hat{e}_2 &= r_{12} \hat{e}_X + r_{22} \hat{e}_Y + r_{32}\hat{e}_Z \tag{1} \\ \hat{e}_3 &= r_{13} \hat{e}_X + r_{23} \hat{e}_Y + r_{33}\hat{e}_Z \end{align} \] Then, the rotation matrix \({}^s\mathbf{R}_b\in\mathbb{R}^{3\times3}\) is defined by: \[ {}^s\mathbf{R}_b = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} \tag{2} \] If the rotation matrix expressed frame \(\{B\}\) with respect to frame \(\{S\}\), we use (pre)superscript \(s\) and (post)subscript \(b\) on the rotation matrix. For notation simplicity, we often suppress the superscript/subscript of the rotation matrix. However, if necessary, we emphasize the superscript/subscript notations of rotation matrix for clarification, and for other reasons which we show later.

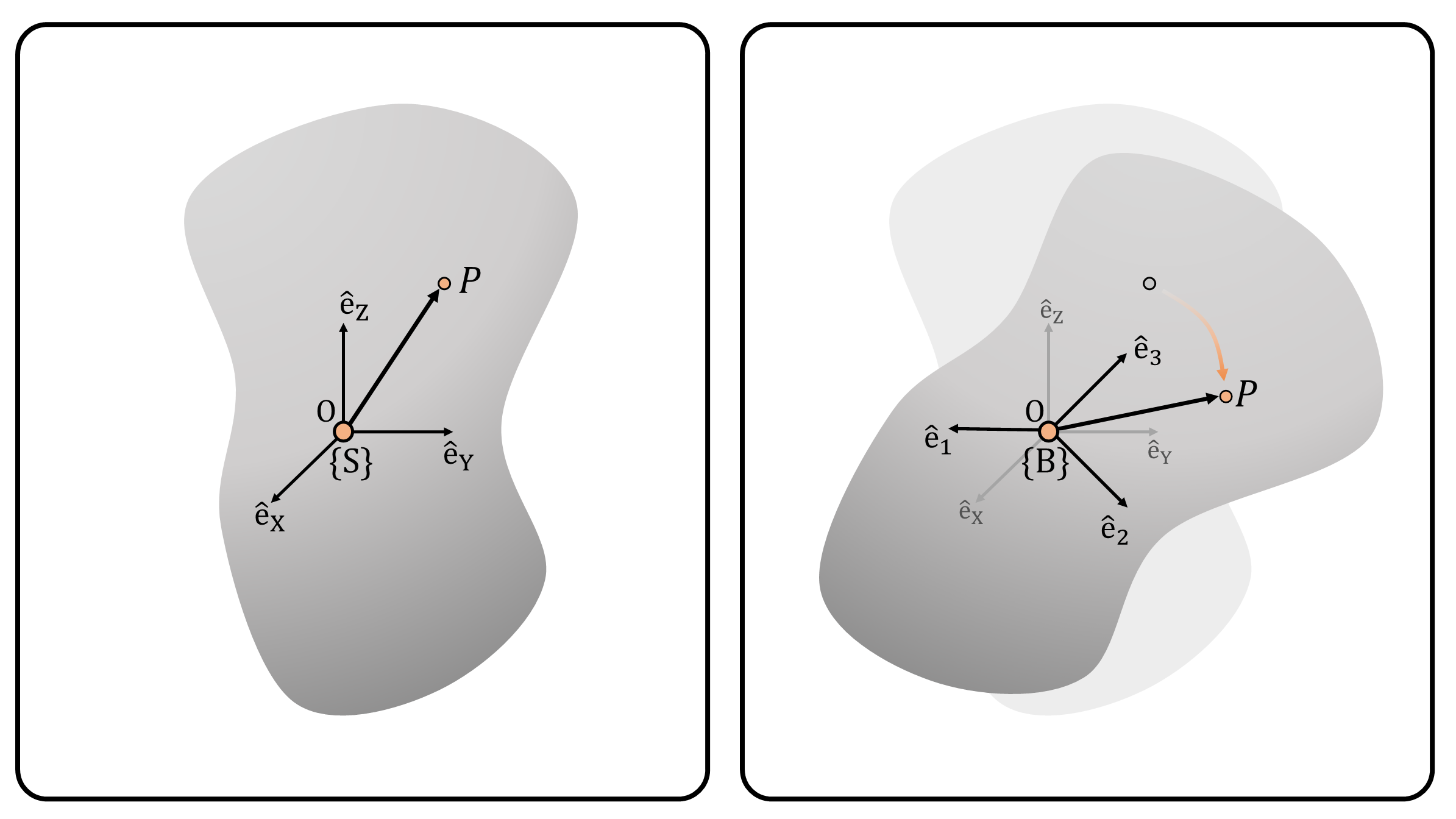
(Figure 1) (Left) A rigid object that is fixed at point \(O\). A fixed, inertial frame \(\{S\}\) consists of three orthonormal basis vectors \(\hat{e}_X,\hat{e}_Y,\hat{e}_Z\). (Right) A rigid object before and after rotation. A body-fixed frame \(\{B\}\) consists of three new orthonormal basis vectors \(\hat{e}_1,\hat{e}_2,\hat{e}_3\) that is the rotation of the original basis vectors \(\hat{e}_X,\hat{e}_Y,\hat{e}_Z\), respectively.

Two Main Properties of Rotation Matrices

Two main properties exist for rotation matrices.

• Rotation matrix is an orthogonal matrix
• The determinant of a rotation matrix is +1.

Here, we show that property 1 corresponds to property 1 of rigid body transformation, where length is preserved under rigid body motion. And property 2 correspond to property 2 of rigid body transformation, where the cross product between any two vectors is preserved under rigid body motion.

Property 1 – Rotation Matrix is an Orthogonal Matrix

Since the bases of frame \(\{S\}\) are mutually orthonormal, the bases of frame \(\{B\}\) are also mutually orthonormal: \[ \hat{e}_i \cdot \hat{e}_j = \delta_{ij} ~~~~~~ i,j\in\{1,2,3\} \] In this equation, \(\delta_{ij}\) is the Kronecker delta symbol.

From equation 1, we can derive: \[ \mathbf{RR}^{\text{T}} = \mathbf{I}_{3} = \mathbf{R}^{\text{T}}\mathbf{R} ~~~~~~~~~~~~ \mathbf{R}^{-1} = \mathbf{R}^{\text{T}} \tag{3} \] In other words, rotation matrix is an orthogonal matrix.

It is immediate that the inverse of rotation matrix \({}^b\mathbf{R}_s\in\mathbb{R}^{3\times3}\), which represents the coordinates of the basis of frame \(\{S\}\) with respect to frame \(\{B\}\), is \({}^s\mathbf{R}_b^{-1}\).¹ This can intuitively derived using the superscript and subscript notation, since if we contract/subtract the adjacent superscript and subscript: \[ \require{cancel} {}^s\mathbf{R}_{\cancel{b}} {}^{\cancel{b}}\mathbf{R}_s = {}^{s}\mathbf{R}_s = \mathbf{I}_3 ~~~~~~~~~~~~~~ {}^b\mathbf{R}_{\cancel{s}} {}^{\cancel{s}}\mathbf{R}_b = {}^{b}\mathbf{R}_b = \mathbf{I}_3 \] It is obvious that representing the coordinates of the basis of frame \(\{S\}\) with its own bases is just an identity matrix \(\mathbf{I}_3\).

Property 2 – Determinant of a Rotation Matrix is +1

After the rotational motion of the rigid object, the right-hand coordinate should still be a right-hand coordinate: \[ \begin{alignat*}{4} & \hat{e}_1\times \hat{e}_2 = \hat{e}_3 ~~~~~~~~~ &&\hat{e}_2\times \hat{e}_3 = \hat{e}_1 ~~~~~~~~~ &&\hat{e}_3\times \hat{e}_1 = \hat{e}_2 \\ & \hat{e}_X\times \hat{e}_Y = \hat{e}_Z ~~~~~~~~~ && \hat{e}_Y\times \hat{e}_Z = \hat{e}_X ~~~~~~~~~ &&\hat{e}_Z\times \hat{e}_X = \hat{e}_Y \end{alignat*} \] From \(\hat{e}_1 \times \hat{e}_2 = \hat{e}_3\) and Equation 1: \[ r_{21}r_{32}-r_{31}r_{22} = r_{13} ~~~~~~~~~~~~~ r_{31}r_{12}-r_{11}r_{32} = r_{23} ~~~~~~~~~~~~~ r_{11}r_{22}-r_{21}r_{12} = r_{33} \] And since \(r_{13}^2+r_{23}^2+r_{33}^2=1\): \[ r_{13}^2+r_{23}^2+r_{33}^2=1 = r_{13}(r_{21}r_{32}-r_{31}r_{22}) + r_{23}( r_{31}r_{12}-r_{11}r_{32}) + r_{33}(r_{11}r_{22}-r_{21}r_{12}) = \det{\mathbf{R}} \tag{4} \] Thus, the determinant of a rotation matrix is +1.

Special Orthogonal Group SO(3)

We provide a formal definition of rotation matrix. The set of all \(\mathbb{R}^{3\times 3}\) matrices which satisfy the two properties above is called the Special Orthogonal Group, which is denoted as \(SO(3)\): \[ SO(3) = \{ \mathbf{R}\in \mathbb{R}^{3\times 3}: \mathbf{RR^T}=\mathbf{I}, \;\;\; \det{\mathbf{R}}=+1 \} \] In other words, a rotation matrix is a special orthogonal matrix. Adjective special comes from the fact that rotation matrix is a subset of orthogonal matrix, since we only consider orthogonal matrix with determinant value +1.²

Two Perspectives on Rotation Matrices

When a rotation matrix \({}^{s}\mathbf{R}_{b}\) (or \(\mathbf{R}\)) is multiplied by a vector in \(\mathbf{R}^3\) space, there are two interpretation. One interpretation is a passive transformation of a vector and the other is an active transformation of a vector. For passive transformation, we emphasize the superscript/subscript notation of the rotation matrix. For active transformation, we suppress the superscript/subscript notation. Moreover, it is worth emphasizing that this section introduces two different perspectives of the identical result.

Perspective 1 – Passive Transformation

Consider an arbitrary point \(P\), which is located at \(\mathbf{p}\) measured from the origin (Figure 2, Left). Consider two frames \(\{S\}\) and \(\{B\}\), where the relative orientation is expressed as \({}^{s}\mathbf{R}_b\).

Under frame \(\{S\}\), the components of \(\mathbf{p}\) are:: \[ {}^s\mathbf{p} = p_x \hat{e}_X + p_y \hat{e}_Y + p_z \hat{e}_Z \] In this equation, superscript \(s\) is used to emphasize the components of \(\mathbf{p}\) is represented with respect to frame \(\{S\}\).

Under frame \(\{B\}\), the components of \(\mathbf{p}\) are:: \[ {}^{b}\mathbf{p} = p_x' \hat{e}_1 + p_y' \hat{e}_2 + p_z' \hat{e}_3 \] By expressing bases \(\hat{e}_1,\hat{e}_2,\hat{e}_3\) with respect to \(\hat{e}_X,\hat{e}_Y,\hat{e}_Z\) and match the components of the bases \(\hat{e}_X,\hat{e}_Y,\hat{e}_Z\), we have: \[ \begin{align} p_x &= p_x'r_{11} + p_y'r_{12} + p_z'r_{13} \\ p_y &= p_x'r_{21} + p_y'r_{22} + p_z'r_{23} \\ p_z &= p_x'r_{31} + p_y'r_{32} + p_z'r_{33} \end{align} \;\;\;\;\; \underbrace{ \begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix} }_{{}^{s}\mathbf{p}} = \underbrace{ \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \\ \end{bmatrix} }_{{}^{s}\mathbf{R}_{b}} \underbrace{ \begin{bmatrix} p_x' \\ p_y' \\ p_z' \end{bmatrix} }_{{}^b\mathbf{p}}, \;\;\;\; {}^{s}\mathbf{p} = {}^{s}\mathbf{R}_{b} \; {}^{b}\mathbf{p} \tag{5} \] In other words, when a rotation matrix \({}^{s}\mathbf{R}_{b}\) is applied to an element of \(\mathbb{R}^{3}\), it transforms the components expressed in frame \(\{B\}\) to frame \(\{S\}\). This is a perspective of passive transformation of a rotation matrix, since given a fixed \(\mathbf{p}\), the rotation matrix changes the components of \(\mathbf{p}\) initially expressed in frame \(\{S\}\) to frame \(\{B\}\). Hence for a perspective of passive transformation, we emphasize the superscript/subscript of the rotation matrix.

Perspective 2 – Active Transformation

Passive transformation fixes \(\mathbf{p}\) and changes the frame of reference in which the components of \(\mathbf{p}\) is represented. Another interpretation is fixing the frame which represents \(\mathbf{p}\), and apply a transformation (or rotation) to \(\mathbf{p}\) (Figure 2, Right). As much as we rotate frame \(\{S\}\) to match frame \(\{B\}\), applying \({}^{s}\mathbf{R}_{b}\) to \(\mathbf{p}\) rotates \(\mathbf{p}\) to a new position \(\mathbf{p}'\): \[ \mathbf{p}' = \mathbf{R}\mathbf{p} \]
Since we are fixing the frame of reference, we suppress the superscript/subscript of rotation matrix, \(\mathbf{p}\) and \(\mathbf{p}'\). For a given rotation matrix \(\mathbf{R}\), a natural question which may emerge is the corresponding (1) axis of rotation and (2) the rotated angle about it. We intentionally defer that discussion to our next post.

Summarizing, when a rotation matrix is applied to an element of \(\mathbb{R}^{3}\), there are two perspectives: passive transformation and active transformation of the \(\mathbb{R}^3\) element. It is very important to be cognizant that it provides two different perspectives of the same result. We are viewing the same mountain from a different perspective.

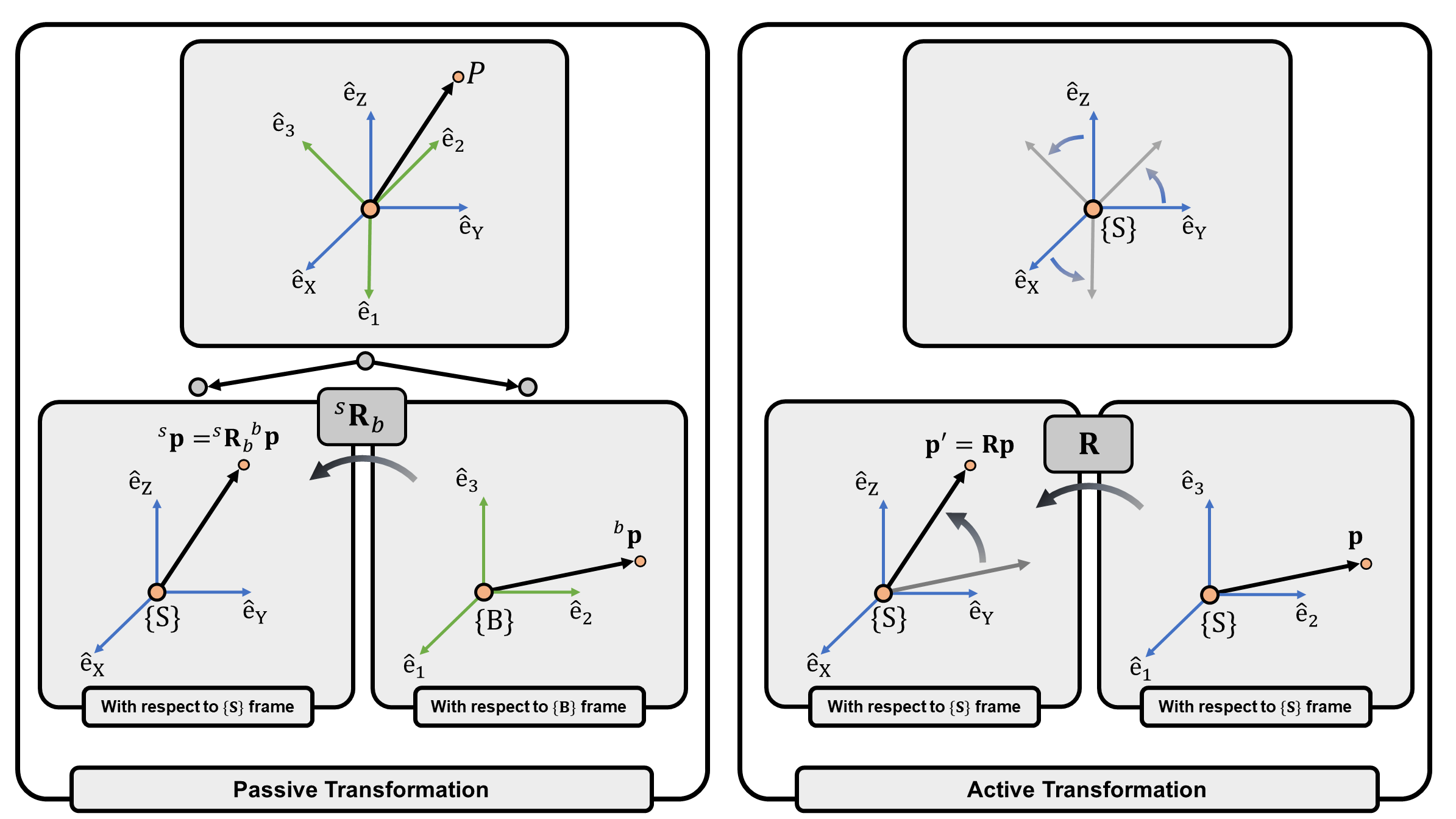
(Figure 2) (Left) Passive transformation of rotation matrix. (Right) Active transformation of rotation matrix.

Rotation Matrix is a Rigid Body Transformation

We show that a rotation matrix \(\mathbf{R}\) is a rigid body transformation. Recall that a map \(\mathbf{g}(\cdot): \mathbb{R}^3\rightarrow \mathbb{R}^3\) is called a rigid body transformation, if [1]:

• Length is preserved: \(\forall \mathbf{p}, \mathbf{q}\in\mathbb{R}^3: ||\mathbf{p-q}|| = || \mathbf{g}(\mathbf{p})-\mathbf{g}(\mathbf{q})||\)
• Cross product between vectors is preserved: \(\forall \mathbf{v}, \mathbf{w}\in\mathbb{R}^3: \mathbf{g}(\mathbf{v}\times\mathbf{w})= \mathbf{g}(\mathbf{v})\times\mathbf{g}(\mathbf{w})\)

Rotation Matrix Preserves Length

Consider \(\mathbf{p}\in\mathbb{R^3}\). We apply a rotation matrix to \(\mathbf{p}\) which results in \(\mathbf{p}'=\mathbf{Rp}\in\mathbb{R}^3\). Since rotation matrix is an orthogonal matrix (Equation ), it is immediate to show that the square length of \(\mathbf{p}\) and \(\mathbf{p}'\) are identical: \[ ||\mathbf{p}||^2 = \mathbf{p^T}\mathbf{p} = \mathbf{p^T}\mathbf{I}_3\mathbf{p} = \mathbf{p^TR^T}\mathbf{R}\mathbf{p} = \mathbf{p'^{\text{T}}}\mathbf{p}'= ||\mathbf{p}'||^2 \]

Rotation Matrix Preserves Cross Product between two Vectors

Before showing this, we show a well-known identity.³ Let \(\mathbf{R}\) be a rotation matrix, and \(\mathbf{v}\in\mathbb{R}^3\). Then: \[ \mathbf{R}[\mathbf{v}]\mathbf{R}^{\text{T}} = [\mathbf{Rv}] \] where \([\;\cdot\;]:\mathbb{R}^{3}\rightarrow\mathbb{R}^{3\times 3}\) is the matrix representation of the cross product of a \(\mathbb{R}^3\).⁴

Consider \(\mathbf{v},\mathbf{w}\in\mathbb{R^3}\). Then: \[ \mathbf{R}(\mathbf{v}\times \mathbf{w})= \mathbf{R}[\mathbf{v}]\mathbf{w}=\mathbf{R}[\mathbf{v}]\mathbf{R^T}\mathbf{R}\mathbf{w}=[\mathbf{Rv}]\mathbf{Rw} = \mathbf{Rv}\times\mathbf{Rw} \] Thus, rotation matrix preserves cross product between two vectors.

References

[1]

R. M. Murray, Z. Li, and S. S. Sastry, A mathematical introduction to robotic manipulation. CRC press, 2017, p. 21.

---

1. We leave it as an exercise with a hint: \[ \hat{e}_i \cdot \hat{e}_X = \hat{e}_X \cdot \hat{e}_i = r_{1i}, ~~~~ \hat{e}_i \cdot \hat{e}_Y = \hat{e}_Y \cdot \hat{e}_i = r_{2i} ~~~~ \hat{e}_i \cdot \hat{e}_Z = \hat{e}_Z \cdot \hat{e}_i = r_{3i} ~~~~~~~ i\in\{1,2,3\} \]↩︎

2. It is quick to show that for an orthogonal matrix: \[ \mathbf{RR^T} = \mathbf{I} ~~~~~~~~~ \det(\mathbf{RR^T}) = \det{\mathbf{R}}^2 = 1 ~~~~~~~~~ \det{\mathbf{R}}=\pm 1 \] Within the orthogonal matrix, we choose matrices with determinant value +1. ↩︎

3. In this post, we defer the detailed proof of this identity. A detailed discussion is provided when we discuss about \(SO(3)\) Lie Group and its corresponding Lie Algebra.↩︎

4. You might find this footnote useful↩︎