Rigid Body Transformation
Moses C. Nah
2023-03-03
Introduction
A rigid body (or object) is a collection of particles that the distances between the particles do not change as the body moves and/or rotates. In other words, a rigid body is an idealized object that do not deform or bend under the influence of external forces. A rigid body is an idealization, as all materials have some degree of elasticity and deform to some extent when subjected to external forces. Nevertheless, rigid body assumption is a useful simplification for the analysis of the kinematics/dynamics of rigid objects.
In robotics, an often used model is a set of rigid bodies connected by moving pair. To fully understand the dynamics (or mechanics) of such model, one must focus on rigid body motion and its interactions with other bodies which consist the robotic system—often called multi-body dynamics. As a first crucial step to study multi-body dyanamics, we study about rigid body transformation.
Properties of Rigid Body Motion
The two main properties of rigid body motion (or transformation) is:
- The length between any two points of the rigid object is preserved.
- The cross produce between any two vectors is preserved.
Property 1 – Length is Preserved
Consider a two points \(P\) and \(Q\) attached to a rigid body (Figure 1). To specify the position of the point \(P\) and \(Q\), we define a fixed, inertial frame \(\{S\}\). Let the position of point \(P\) and \(Q\) be \(\mathbf{p}(t)\) and \(\mathbf{q}(t)\in\mathbb{R}^3\), respectively. The positions of point \(P\) and \(Q\) are parameterized with time \(t\).
By definition of rigid object, the length (or distance) between two points always remains the same: \[ \forall t>0: ~~ || \mathbf{p}(t)-\mathbf{q}(t) || = C \] In this equation, \(C\) is a constant value, and \(||\cdot||:\mathbb{R}^3\rightarrow \mathbb{R}^{+}\) denotes the Euclidean distance between two points.1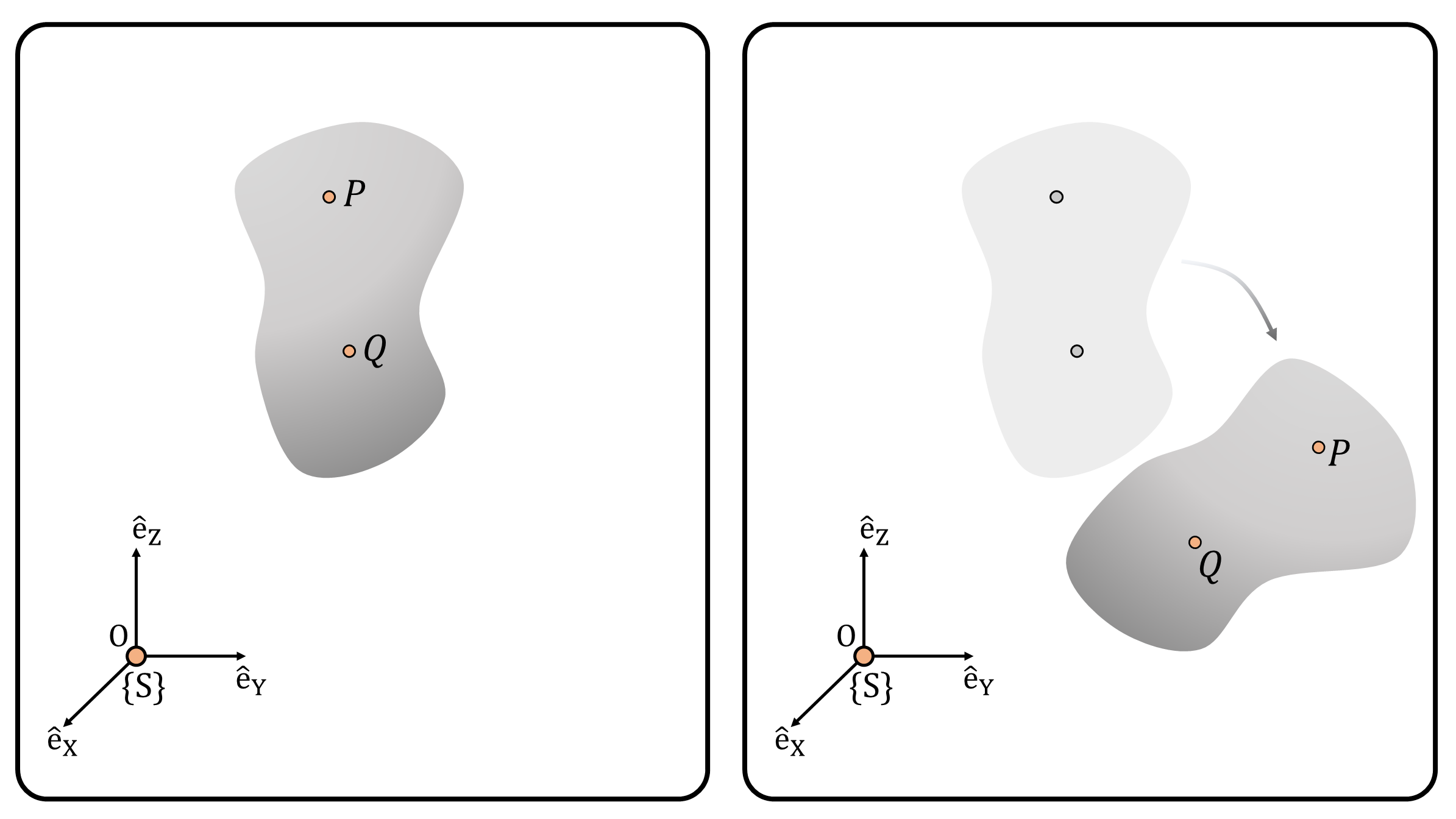
(Figure 1) A rigid object and frame \(\{S\}\), which consists of basis vectors \(\hat{e}_X, \hat{e}_Y, \hat{e}_Z\). (Right) A rigid body motion of the rigid object.
Property 2 – Cross Product between Vectors is Preserved
While property 1 seems enough to formalize the definition of rigid body motion, one should be aware that property 1 is not yet sufficient. The reason is because property 1 also allows internal reflections, which are not physically realizable [1]. While reflection preserves the length of the rigid object, the reflected object is different from the previous object (cf. enantiomer) (Figure 2). To preclude this case, an additional property of rigid body motion is that the cross product between vectors should be preserved.
This can be checked immediate from the example shown in Figure 2. For the object on the left, it is clear that \(\hat{e}_X\times \hat{e}_Y=\hat{e}_Z\). As reflection changes \(\hat{e}_X, \hat{e}_Y\) to \(\hat{e}_X', \hat{e}_Y'\), then \(\hat{e}_X'\times \hat{e}_Y'=-\hat{e}_Z\)—the cross-produce is not preserved and the sign is flipped.
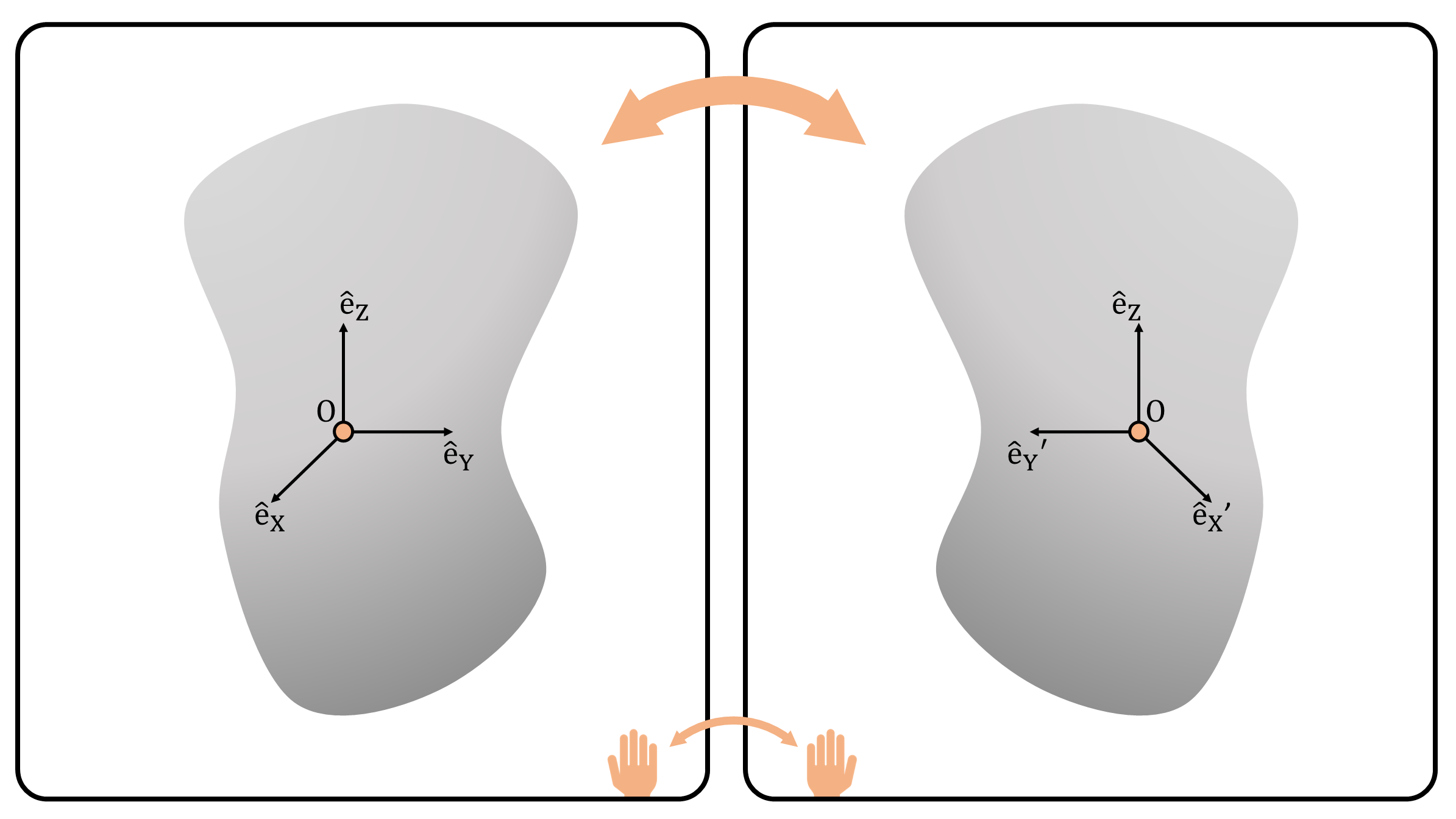
(Figure 2) While reflection preserves the length and shape of the rigid object, the orientation changes and results in a different object. As shown in the figure, a right-handed coordinate frame changes to a left-handed coordinate frame.
Formal Definition of Rigid Body Transformation
Based on property 1 and 2, we derive a formal definition of rigid body transformation. A map \(\mathbf{g}(\cdot): \mathbb{R}^3\rightarrow \mathbb{R}^3\) is called a rigid body transformation, if [1]:
- Length is preserved: \(\forall \mathbf{p}, \mathbf{q}\in\mathbb{R}^3: ||\mathbf{p-q}|| = || \mathbf{g}(\mathbf{p})-\mathbf{g}(\mathbf{q})||\)
- Cross product between vectors is preserved: \(\forall \mathbf{v}, \mathbf{w}\in\mathbb{R}^3: \mathbf{g}(\mathbf{v}\times\mathbf{w})= \mathbf{g}(\mathbf{v})\times\mathbf{g}(\mathbf{w})\)
A Quick Remark
Note that \(\mathbf{g}(\cdot)\) is a linear operator between two (vector) spaces \(\mathbb{R}^3\): \[ \begin{align*} \forall \mathbf{v},\mathbf{w}\in\mathbb{R}^3&: ~~\mathbf{g}(\mathbf{v}+\mathbf{w}) = \mathbf{g}(\mathbf{v}) + \mathbf{g}(\mathbf{w}) \\ \forall \lambda \in \mathbb{R}, ~ \forall \mathbf{v}\in\mathbb{R}^3 &: ~~\mathbf{g}(\lambda\mathbf{v}) = \lambda \mathbf{g}(\mathbf{v}) \end{align*} \]
Moreover, the equivalent statement for the first property is the absolute angle between two vectors are preserved. We know that: \[ \begin{align*} \begin{split} ||\mathbf{p+q}||^2 - ||\mathbf{p-q}||^2 &= 4\mathbf{p}\cdot\mathbf{q} \\ ||\mathbf{g}(\mathbf{p+q})||^2 - ||\mathbf{g}(\mathbf{p-q})||^2 &= 4\mathbf{g}(\mathbf{p})\cdot\mathbf{g}(\mathbf{q}) \\ \end{split} ~~~~~~ \Longrightarrow ~~~~~ \mathbf{p}\cdot\mathbf{q} = \mathbf{g}(\mathbf{p})\cdot\mathbf{g}(\mathbf{q}) \end{align*} \] In this equation, \(\cdot\) denotes the dot product between two vectors. Hence, the absolute angle between two vectors is preserved. This implies that vectors that are mutually orthogonal are remained to be orthogonal after rigid body transformation.
References
In detail, let \(\mathbf{p}=[p_x, p_y, p_z]\). Then, \(||\mathbf{p}||=\sqrt{p_x^2+p_y^2+p_z^2}\).↩︎