Introduction

In the previous post, we show that rotation matrix \(\mathbf{R}\) is an element of a \(SO(3)\) group, and represents a rigid body transformation. Here, we bridge the relation between rotation matrix \(\mathbf{R}\) and the rotation about a unit axis \(\hat{\boldsymbol{\omega}}\) with angle \(\theta\).



Exponential Coordinates of Rotation Matrix

Consider \(\mathbf{p}\in\mathbb{R}^3\) which rotates about unit axis \(\hat{\boldsymbol{\omega}}\). We define a fixed, inertial frame \(\{S\}\) to describe the components of \(\mathbb{R}^3\), and for notational simplicity, we omit the superscript \(s\).

It is well-known that the velocity of \(\mathbf{p}\) is defined by (Figure 1, Left): \[ \dot{\mathbf{p}} = \hat{\boldsymbol{\omega}} \times \mathbf{p} \]

The cross product of \(\hat{\boldsymbol{\omega}}\) can be expressed in matrix form: \[ \hat{\boldsymbol{\omega}}= \begin{pmatrix} \hat{\omega}_x \\ \hat{\omega}_y \\ \hat{\omega}_z \end{pmatrix} ~~~~~~ [\hat{\boldsymbol{\omega}}]= \begin{pmatrix} 0 & -\hat{\omega}_z & \hat{\omega}_y \\ \hat{\omega}_z & 0 & -\hat{\omega}_x \\ -\hat{\omega}_y & \hat{\omega}_x & 0 \end{pmatrix} ~~~~~~ \dot{\mathbf{p}} = [\hat{\boldsymbol{\omega}}]\mathbf{p} \] The resulting equation is a first-order linear differential equation of \(\dot{\mathbf{x}}=\mathbf{Ax}\) form. The closed-form solution for this equation is well-known: \[ \mathbf{p}(t) = \exp([\hat{\boldsymbol{\omega}}]t) ~\mathbf{p}(0) \] In this equation, \(\exp(\cdot):\mathbb{R}^{3\times 3}\rightarrow \mathbb{R}^{3\times 3}\) is called the exponential map defined by: \[ \exp([\hat{\boldsymbol{\omega}}]t) = \mathbf{I}_3 + [\hat{\boldsymbol{\omega}}]t+\frac{1}{2!}[\hat{\boldsymbol{\omega}}]^2t^2 + \cdots + \frac{1}{n!}[\hat{\boldsymbol{\omega}}]^nt^n +\cdots \tag{1} \]
Here, we set \(\theta=t\), i.e., \(\mathbf{p}\) rotates at a constant rate of 1rad/s from \(t=0\) to \(t=\theta\). Hence, \(\exp([\hat{\boldsymbol{\omega}}]\theta)\) transforms \(\mathbf{p}\) by rotating it about \(\hat{\boldsymbol{\omega}}\) with angle \(\theta\).

**(Figure 1)** **(Left)** Rotation of $\mathbf{p}$ about unit axis $\hat{\boldsymbol{\omega}}$. **(Right)** Rotation of $\mathbf{p}$ about unit axis $\hat{\boldsymbol{\omega}}$ with angle $\theta$.

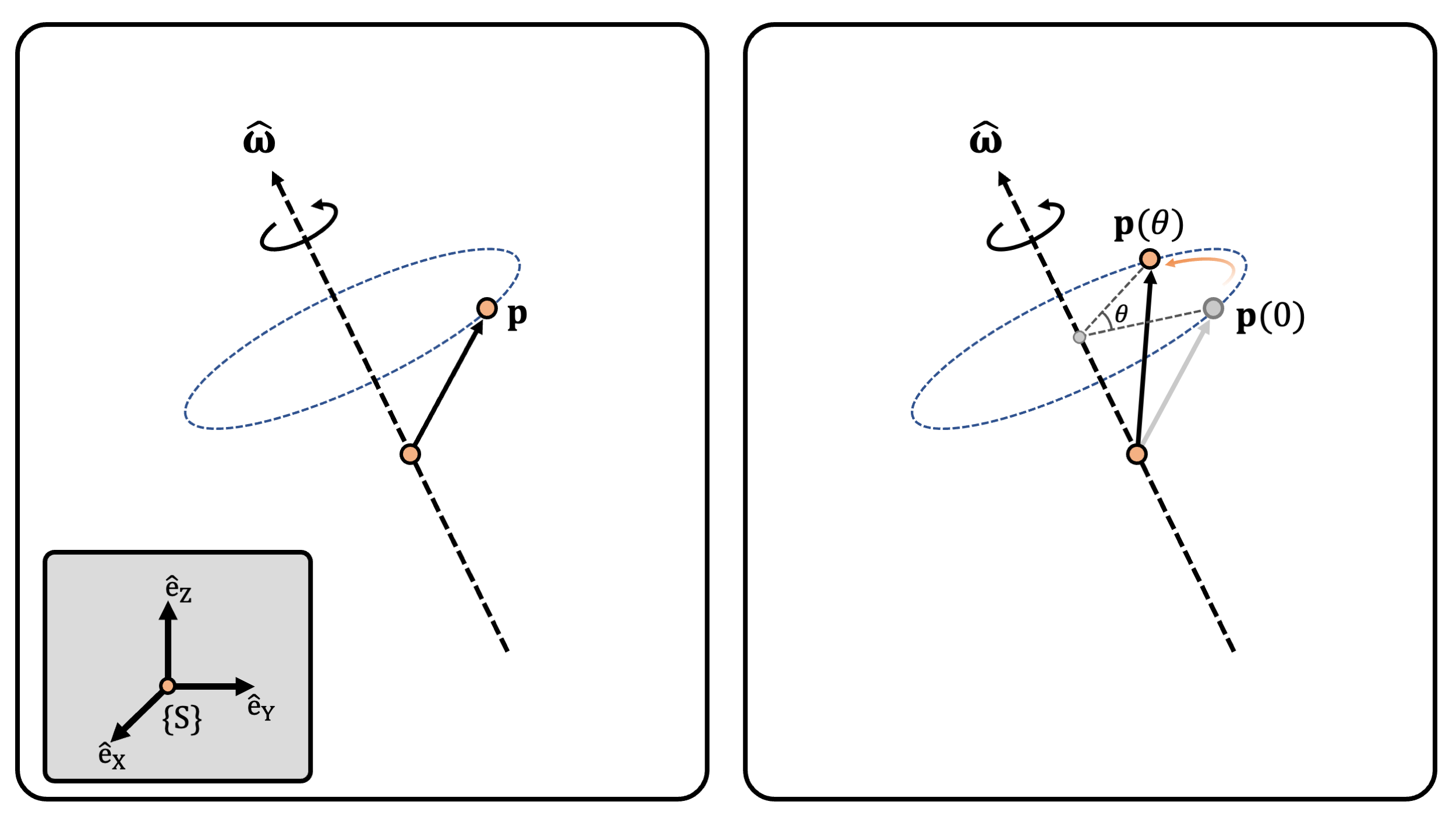
(Figure 1) (Left) Rotation of \(\mathbf{p}\) about unit axis \(\hat{\boldsymbol{\omega}}\). (Right) Rotation of \(\mathbf{p}\) about unit axis \(\hat{\boldsymbol{\omega}}\) with angle \(\theta\).



Since \([\hat{\boldsymbol{\omega}}]\) is a \(\mathbb{R}^{3\times 3}\) matrix, based on Cayley-Hamilton theorem, all the terms with order higher than 3 can be expressed as a sum of \(\mathbf{I}_3, [\hat{\boldsymbol{\omega}}], [\hat{\boldsymbol{\omega}}]^2\). Based on the characteristic equation of \([\hat{\boldsymbol{\omega}}]\), we have: \[ \det(\lambda\mathbf{I}-[\hat{\boldsymbol{\omega}}]) = \lambda^3 + (\hat{\omega}_x^2+\hat{\omega}_y^2+\hat{\omega}_z^2)\lambda = \lambda^3+\lambda ~~~~~~~~~~~~~~~ [\hat{\boldsymbol{\omega}}]^3=-[\hat{\boldsymbol{\omega}}] \] The infinite sum of Equation 1 can be simplified: \[ \begin{align*} \exp([\hat{\boldsymbol{\omega}}]\theta) &= \mathbf{I}_3 + [\hat{\boldsymbol{\omega}}]\theta+\frac{1}{2!}[\hat{\boldsymbol{\omega}}]^2\theta^2 + \cdots + \frac{1}{n!}[\hat{\boldsymbol{\omega}}]^n\theta^n +\cdots \\ &= \mathbf{I}_3 + [\hat{\boldsymbol{\omega}}]\theta + \frac{1}{2!}[\hat{\boldsymbol{\omega}}]^2\theta^2 - \frac{1}{3!}[\hat{\boldsymbol{\omega}}]\theta^3 - \frac{1}{4!}[\hat{\boldsymbol{\omega}}]^2\theta^2+ \cdots \\ &= \mathbf{I}_3 + [\hat{\boldsymbol{\omega}}]\Big(\theta-\frac{1}{3!}\theta^3+\cdots\Big) + [\hat{\boldsymbol{\omega}}]^2\Big( \frac{\theta^2}{2!}-\frac{\theta^4}{4!}+\cdots \Big) \\ &= \mathbf{I}_3 + \sin\theta[\hat{\boldsymbol{\omega}}] + (1-\cos\theta)[\hat{\boldsymbol{\omega}}]^2 \end{align*} \] This is the famous Rodrigues’ rotation formula: \[ \exp([\hat{\boldsymbol{\omega}}]\theta)= \mathbf{I}_3 + \sin\theta[\hat{\boldsymbol{\omega}}] + (1-\cos\theta)[\hat{\boldsymbol{\omega}}]^2 \tag{2} \]

Rodrigues’ Rotation Formula

In fact, the more well-known Rodrigues’ formula is as follows: \[ \mathbf{v}' = \mathbf{v}\cos\theta + (\hat{\boldsymbol{\omega}}\times\mathbf{v})\sin\theta + \hat{\boldsymbol{\omega}}(\hat{\boldsymbol{\omega}} \cdot \mathbf{v})(1-\cos\theta) \tag{3} \] In this equation, \(\mathbf{v}\) is mapped to \(\mathbf{v}'\) by rotating \(\mathbf{v}\) about unit axis \([\hat{\boldsymbol{\omega}}]\) with angle \(\theta\). We show that Equation 3 can be derived from Equation 2. Before that, we introduce the following identity:1 \[ [\hat{\boldsymbol{\omega}}]^2 = \hat{\boldsymbol{\omega}}\hat{\boldsymbol{\omega}}^{\mathbf{T}}-||\hat{\boldsymbol{\omega}}||^2\mathbf{I}_3 = \hat{\boldsymbol{\omega}}\hat{\boldsymbol{\omega}}^{\mathbf{T}}-\mathbf{I}_3 \] Multiplying Equation 2 with \(\mathbf{v}\in\mathbb{R}^3\) results in Equation 3: \[ \begin{align*} \exp([\hat{\boldsymbol{\omega}}]\theta) \mathbf{v} &= \mathbf{v}+ \sin\theta[\hat{\boldsymbol{\omega}}]\mathbf{v} + (1-\cos\theta)[\hat{\boldsymbol{\omega}}]^2 \mathbf{v} = \mathbf{v} + (\hat{\boldsymbol{\omega}} \times \mathbf{v})\sin\theta + (1-\cos\theta)( \hat{\boldsymbol{\omega}}\hat{\boldsymbol{\omega}}^{\mathbf{T}}\mathbf{v} - \mathbf{v} ) \\ &= \cos\theta \mathbf{v}+(\hat{\boldsymbol{\omega}} \times \mathbf{v})\sin\theta + \hat{\boldsymbol{\omega}}(\hat{\boldsymbol{\omega}}\cdot\mathbf{v})(1-\cos\theta) \end{align*} \]



A Quick Example

Consider we rotate \(\mathbf{p}\) about the unit \(\mathrm{\hat{e}_Z}\) axis with angle \(\theta\). Then, \(\hat{\boldsymbol{\omega}}=(0,0,1)\), and by definition: \[ [\hat{\boldsymbol{\omega}}]= \begin{pmatrix} 0 & -\hat{\omega}_z & \hat{\omega}_y \\ \hat{\omega}_z & 0 & -\hat{\omega}_x \\ -\hat{\omega}_y & \hat{\omega}_x & 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} ~~~~~~~~ [\hat{\boldsymbol{\omega}}]^2 = \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{pmatrix} \] Using the Rodrigues’ formula: \[ \exp([\hat{\boldsymbol{\omega}}]\theta)= \mathbf{I}_3 + \sin\theta \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} + (1-\cos\theta) \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \phantom{-}\cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \] The result is the well-known form.



The Exponential Map is Surjective onto SO(3) [1]

We show that \(\exp([\hat{\boldsymbol{\omega}}]\theta)\) is an element of Special Orthogonal group, SO(3). The proof is straightforward, since all we need to check is (1) \(\exp([\hat{\boldsymbol{\omega}}]\theta)\) is an orthogonal matrix and (2) determinant value of \(\exp([\hat{\boldsymbol{\omega}}]\theta)\) is 1.


Proof 1

Based on Rodrigues’ formula (Equation 2), the transpose of \(\exp([\hat{\boldsymbol{\omega}}]\theta)\) is: \[ \exp([\hat{\boldsymbol{\omega}}]\theta)^{\textbf{T}} = \mathbf{I}_3 - \sin\theta [\hat{\boldsymbol{\omega}}] + (1-\cos\theta)[\hat{\boldsymbol{\omega}}]^2 = \exp(-[\hat{\boldsymbol{\omega}}]\theta) \] If we simply multiply \(\exp([\hat{\boldsymbol{\omega}}]\theta)\) with \(\exp([\hat{\boldsymbol{\omega}}]\theta)^{\textbf{T}}\), and use Cayley-Hamilton’s theorem: \[ \begin{align*} \exp([\hat{\boldsymbol{\omega}}]\theta) \exp([\hat{\boldsymbol{\omega}}]\theta)^{\textbf{T}} &= \{ \mathbf{I}_3 - \sin\theta [\hat{\boldsymbol{\omega}}] + (1-\cos\theta)[\hat{\boldsymbol{\omega}}]^2 \} \{ \mathbf{I}_3 + \sin\theta [\hat{\boldsymbol{\omega}}] + (1-\cos\theta)[\hat{\boldsymbol{\omega}}]^2 \} \\ &= \mathbf{I}_3 + [\hat{\boldsymbol{\omega}}]^2( 2-2\cos\theta-\sin^2\theta ) + [\hat{\boldsymbol{\omega}}]^4(1-\cos\theta)^2 = \mathbf{I}_3 \end{align*} \]


Proof 2

Using Jacobi’s formula: \[ \det( \exp([\hat{\boldsymbol{\omega}}]\theta) ) = \exp( ~ \text{tr}( [\hat{\boldsymbol{\omega}}]\theta ) ~ ) = \exp( 0 ) = 1 \] Hence, \(\exp([\hat{\boldsymbol{\omega}}]\theta)\) is an element of \(SO(3)\) group.



Some Properties

Based on Rodrigues’ formula (Equation 2), we can show some major properties of \(\exp([\hat{\boldsymbol{\omega}}]\theta)\). We leave it as an exercise to the readers:



References

[1]
R. M. Murray, Z. Li, and S. S. Sastry, A mathematical introduction to robotic manipulation. CRC press, 2017, p. 29.

  1. Note that this equation appears when we define the moment of inertia of a rigid object↩︎