Introduction

So far, we have discussed about Newton’s Laws of motion with respect to an inertial reference frame— a frame of reference which is at rest or which is moving at a constant speed in a straight line. While a wide ranges of motion of a system can be analyzed with respect to an inertial reference frame, there are often cases where the motion should be analyzed with respect to a non-inertial reference frame. For instance, as a resident of planet earth which rotates, in principle, all of us should be regarded as a non-inertial reference frame.

Here, we discuss about the Newton’s Laws of motion with respect to a non-inertial reference frame. It is no doubt that the Newton’s Laws of motion is violated, since the laws are described with respect to an inertial reference frame. Nevertheless, by introducing fictitious forces, which are non-physical forces, Newton’s Laws of motion can be generalized to non-inertial frame of reference. For instance, inertial forces1 or Coriolis/centrifugal forces are famous examples of fictitious forces. In this post, We discuss about fictitious forces in great detail.



A Pendulum Hanging on an Accelerating Bus


Inertial Reference Frame

Consider a pendulum with a suspended point mass \(m\) hanging on an accelerating bus (Figure 1). A person standing outside the bus (and therefore can be considered as an inertial frame of reference \(\{S\}\)), is observing the point mass \(m\) (Figure 1, Top).

Based on Newton’s Second Law of motion: \[ \mathbf{T} - m\mathbf{g} = m\mathbf{a} \tag{1} \] While the tension balances the gravitation force along \(\mathrm{\hat{e}_Y}\), the tension along \(\mathrm{\hat{e}_X}\) accelerates the mass \(m\) — absolutely consistent with Newton’s Laws of motion and our physical intuition.



Non-inertial Reference Frame

On the other hand, consider a person sitting in the bus, i.e., the person is accelerating and can be considered as a non-inertial frame of reference \(\{B\}\). Since the person is accelerating, Newton’s Second law of motion is violated — the tension \(\mathbf{T}\) and gravitational force \(-m\mathbf{g}\) are obviously not in balance but mass \(m\) is at rest with respect to the person.

Hence, the person sitting in the bus feels like another force is pulling back the pendulum, which thereby achieves equilibrium. This fictitious force is called inertial force \(-m\mathbf{a}\). \[ \mathbf{T}-m\mathbf{g}+(-m\mathbf{a}) = 0 \tag{2} \] Interestingly, by introducing inertial force \(-m\mathbf{a}\) for the non-inertial reference frame, Newton’s Second law of motion is satisfied. Fictitious forces allow us to use Newton’s Laws of motion even for non-inertial reference frame.

**(Figure 1)** **(Top)** A pendulum hanging on a bus, observed in frame $\{S\}$ which is a fixed, inertial reference frame. **(Bottom)** A pendulum hanging on a bus, observed in frame $\{B\}$ which is a non-inertial reference frame

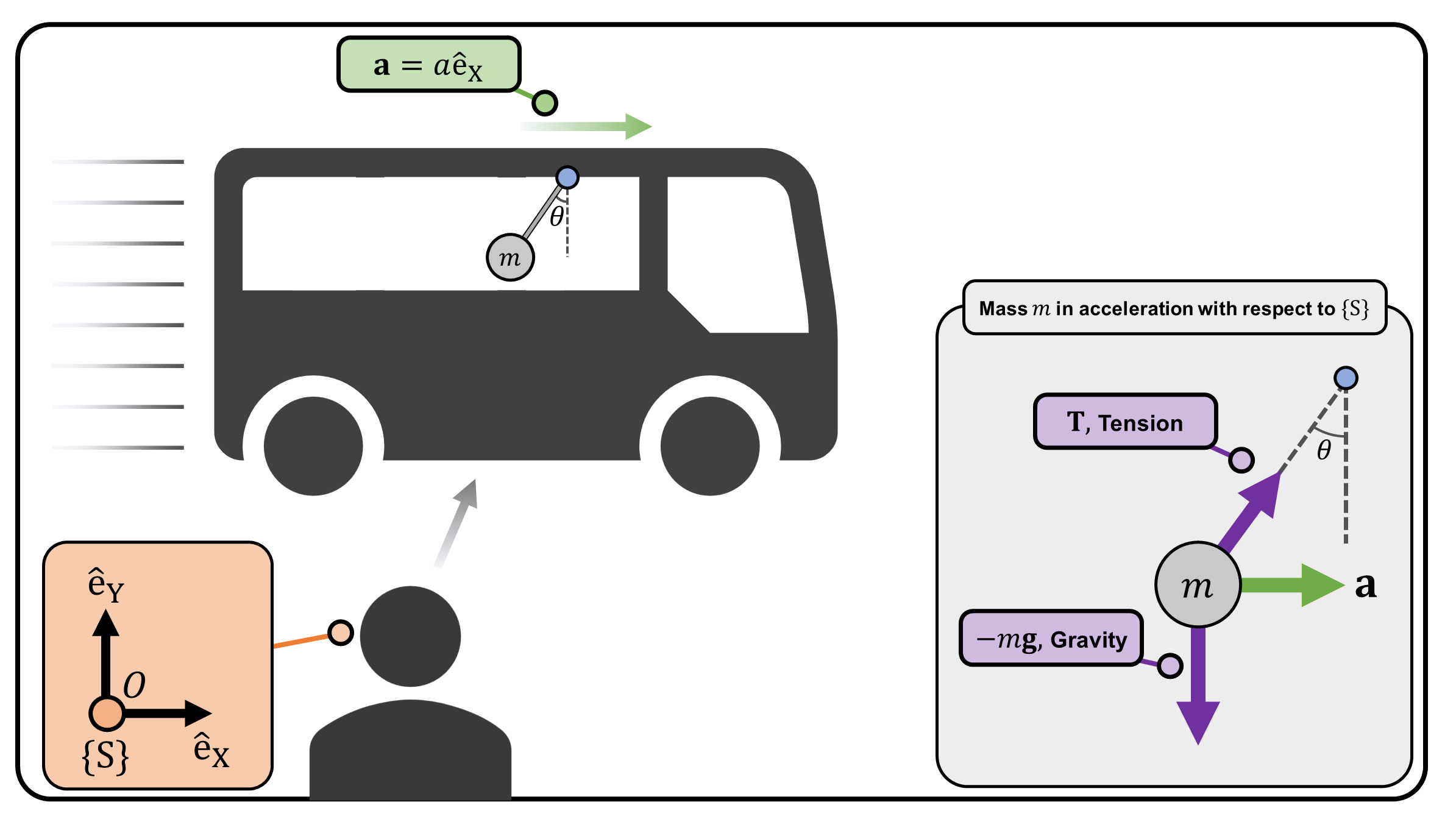
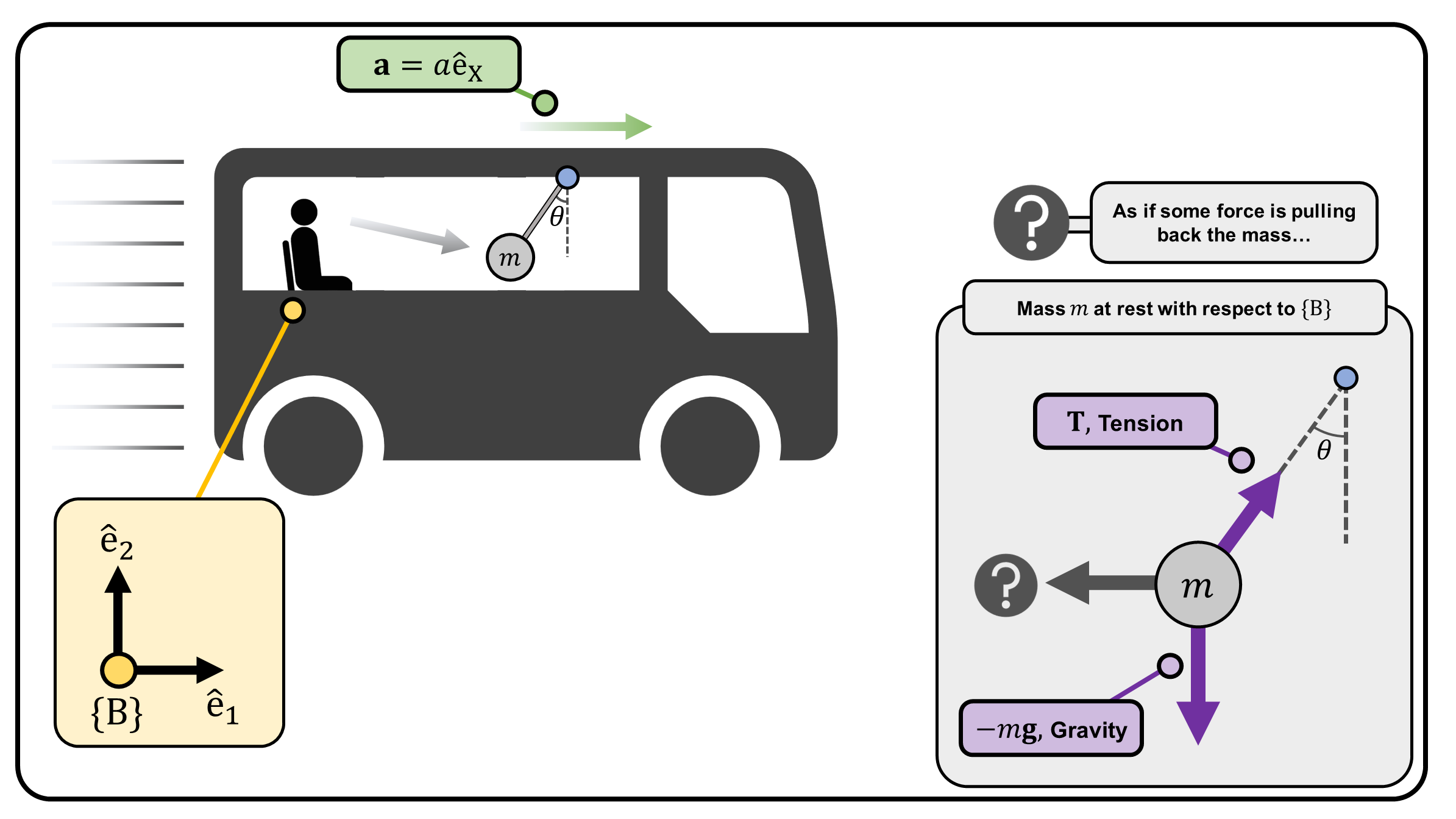
(Figure 1) (Top) A pendulum hanging on a bus, observed in frame \(\{S\}\) which is a fixed, inertial reference frame. (Bottom) A pendulum hanging on a bus, observed in frame \(\{B\}\) which is a non-inertial reference frame



Rotating Reference Frame


Inertial Reference Frame

Consider a particle with mass \(m\) sliding on a frictionless table which is rotating with angular velocity \(\boldsymbol{\omega}\) (Figure 2). A person is standing outside the table (i.e., a fixed, inertial frame \(\{S\}\)), observing the particle. Let the position of mass \(m\) be \(\mathbf{r}\). We express \(\mathbf{r}\) with respect to frame \(\{S\}\), i.e., \(\mathbf{r}=x \mathrm{\hat{e}_X}+y \mathrm{\hat{e}_Y} +z \mathrm{\hat{e}_Z}\).

Since the force along \(\mathrm{\hat{e}_Z}\), i.e., gravity and normal force from the table, is balanced, the net force applied to mass \(m\) is a zero vector. Hence, in inertial reference frame \(\{S\}\), the components \(x\), \(y\), \(z\) is governed by the following differential equations: \[ \sum \mathbf{F}_{ext} = \mathbf{0} = m\mathbf{\ddot{r}} ~~~~ \Longrightarrow ~~~~ m\ddot{x} = 0, ~ m\ddot{y} = 0, ~m\ddot{z} = 0 \] Given the initial position and velocity of mass \(m\), the mass moves in a straight line — absolutely consistent with our physical intuition.

Summarizing, the position, velocity and acceleration of the object is: \[ \begin{align*} \mathbf{r} &= x \mathrm{\hat{e}_X}+y \mathrm{\hat{e}_Y} +z \mathrm{\hat{e}_Z} \\ \mathbf{v} &= \dot{x} \mathrm{\hat{e}_X}+\dot{y} \mathrm{\hat{e}_Y} + \dot{z} \mathrm{\hat{e}_Z}\\ \mathbf{a} &= \ddot{x} \mathrm{\hat{e}_X}+\ddot{y} \mathrm{\hat{e}_Y} + \ddot{z} \mathrm{\hat{e}_Z} \end{align*} \]



Non-inertial Reference Frame

Now, we consider a person sitting on the rotating table (i.e., body-fixed reference frame \(\{B\}\)), observing the particle. We express \(\mathbf{r}\) with respect to frame \(\{B\}\), i.e., \(\mathbf{r}=x'\mathrm{\hat{e}_1}+y' \mathrm{\hat{e}_2} +z' \mathrm{\hat{e}_3}\).

It is no doubt that frame \(\{S\}\) and frame \(\{B\}\) are describing the same \(\mathbf{r}\), but using different bases. In detail:2 \[ \mathbf{r} = x \mathrm{\hat{e}_X}+y \mathrm{\hat{e}_Y} +z \mathrm{\hat{e}_Z} = x'\mathrm{\hat{e}_1}+y' \mathrm{\hat{e}_2} +z' \mathrm{\hat{e}_3} \]

Compared to frame \(\{S\}\) where the bases are fixed in space, the bases of frame \(\{B\}\) rotates with angular velocity \(\boldsymbol{\omega}\). Hence, the time derivative of bases of frame \(\{B\}\) should be considered: \[ \frac{d}{dt}\mathrm{\hat{e}_1} = \boldsymbol{\omega} \times \mathrm{\hat{e}_1} ~~~~~~~~ \frac{d}{dt}\mathrm{\hat{e}_2} = \boldsymbol{\omega} \times \mathrm{\hat{e}_2} ~~~~~~~~ \frac{d}{dt}\mathrm{\hat{e}_3} = \boldsymbol{\omega} \times \mathrm{\hat{e}_3} \] The velocity of the mass, \(\mathbf{v}\) is: \[ \begin{align*} \mathbf{v} = \dot{x} \mathrm{\hat{e}_X}+ \dot{y} \mathrm{\hat{e}_Y} + \dot{z} \mathrm{\hat{e}_Z} &= \dot{x}'\mathrm{\hat{e}_1} +\dot{y}'\mathrm{\hat{e}_2} + \dot{z}'\mathrm{\hat{e}_3} + x' (\boldsymbol{\omega} \times \mathrm{\hat{e}_1}) + y' (\boldsymbol{\omega} \times \mathrm{\hat{e}_2}) + z' (\boldsymbol{\omega} \times \mathrm{\hat{e}_3}) \\ &= \underbrace{\dot{x}'\mathrm{\hat{e}_1} +\dot{y}'\mathrm{\hat{e}_2} + \dot{z}'\mathrm{\hat{e}_3}}_{:=\frac{d'\mathbf{r}}{dt}:=\mathbf{v}'} + \boldsymbol{\omega} \times \underbrace{( x'\mathrm{\hat{e}_1} + y'\mathrm{\hat{e}_2} + z'\mathrm{\hat{e}_3})}_{:=\mathbf{r}} := \frac{d'\mathbf{r}}{dt} + \boldsymbol{\omega} \times \mathbf{r} \end{align*} \] In this equation, we use notation \(d'/dt\) which refers to the rate of change of the components with respect to rotating frame \(\{B\}\) [1]. In other words, \(d'/dt\) only accounts for the time derivative of the components of the rotating frame \(\{B\}\).

Summarizing: \[ \mathbf{v}:= \frac{d\mathbf{r}}{dt} = \frac{d'\mathbf{r}}{dt} + \boldsymbol{\omega} \times \mathbf{r} \tag{3} \] Note that Equation 3 can be generalized to any vector described in frame \(\{B\}\). Moreover, as a person sitting on the rotating table, the observed velocity of mass \(m\) is \(\mathbf{v}'\), not \(\mathbf{v}\).



From Equation 3, the acceleration of the mass \(m\) with respect to frame is straightforward to derive: \[ \require{cancel} \begin{align*} \mathbf{a} = \ddot{x} \mathrm{\hat{e}_X}+\ddot{y} \mathrm{\hat{e}_Y} + \ddot{z} \mathrm{\hat{e}_Z} &= \frac{d\mathbf{v}'}{dt} + \Big(\frac{d\boldsymbol{\omega}}{dt}\Big) \times \mathbf{r} + \boldsymbol{\omega} \times \Big( \frac{d\mathbf{r}}{dt} \Big) \\ &= \frac{d'\mathbf{v'}}{dt} + \boldsymbol{\omega}\times \mathbf{v}' + \Big( \frac{d'\boldsymbol{\omega}}{dt} + \cancel{\boldsymbol{\omega}\times\boldsymbol{\omega}}\Big) \times \mathbf{r} + \boldsymbol{\omega}\times\Big( \underbrace{\frac{d'\mathbf{r}}{dt}}_{:=\mathbf{v}'} + \boldsymbol{\omega} \times \mathbf{r} \Big) \\ &= \frac{d'^2\mathbf{r}}{dt^2} + 2 \big( \boldsymbol{\omega}\times \mathbf{v}' \big) + \frac{d'\boldsymbol{\omega}}{dt} \times \mathbf{r} + \boldsymbol{\omega} \times \big( \boldsymbol{\omega} \times \mathbf{r} \big) \end{align*} \] Summarizing: \[ \mathbf{a} = \mathbf{a}' + 2 \big( \boldsymbol{\omega}\times \mathbf{v}' \big) + \boldsymbol{\alpha}' \times \mathbf{r} + \boldsymbol{\omega} \times \big( \boldsymbol{\omega} \times \mathbf{r} \big) \tag{4} \] \[ \frac{d'^2\mathbf{r}}{dt^2} := \mathbf{a}' = \ddot{x}'\mathrm{\hat{e}_1} + \ddot{y}'\mathrm{\hat{e}_2} + \ddot{z}'\mathrm{\hat{e}_3} ~~~~~~~~ \frac{d'\boldsymbol{\omega}}{dt} := \boldsymbol{\alpha}' =\dot{\omega}_x'\mathrm{\hat{e}_1} + \dot{\omega}_y'\mathrm{\hat{e}_2} + \dot{\omega}_z'\mathrm{\hat{e}_3} \tag{5} \]



As a person sitting on the rotating table, the observed acceleration of mass \(m\) is \(\mathbf{a}'\), not \(\mathbf{a}\). Hence, using the Newton’s Laws of motion with the observed acceleration \(\mathbf{a}'\), there are fictitious forces that are experienced by the person in frame \(\{B\}\), even though the mass is in equilibrium with respect to frame \(\{S\}\). The fictitious forces are derived by multiplying \(m\) on Equation 4: \[ \begin{align*} m\mathbf{a}'&= \underbrace{m\mathbf{a}}_{=\sum\mathbf{F}_{ext}=\mathbf{0}} - 2m \big( \boldsymbol{\omega}\times \mathbf{v}' \big) - m\big(\boldsymbol{\alpha}' \times \mathbf{r}\big) - m\big\{\boldsymbol{\omega} \times \big( \boldsymbol{\omega} \times \mathbf{r} \big) \big\} \\ m\mathbf{a}' &= \mathbf{F}_{Coriolis} + \mathbf{F}_{Euler} + \mathbf{F}_{centrifugal} \end{align*} \tag{5} \]

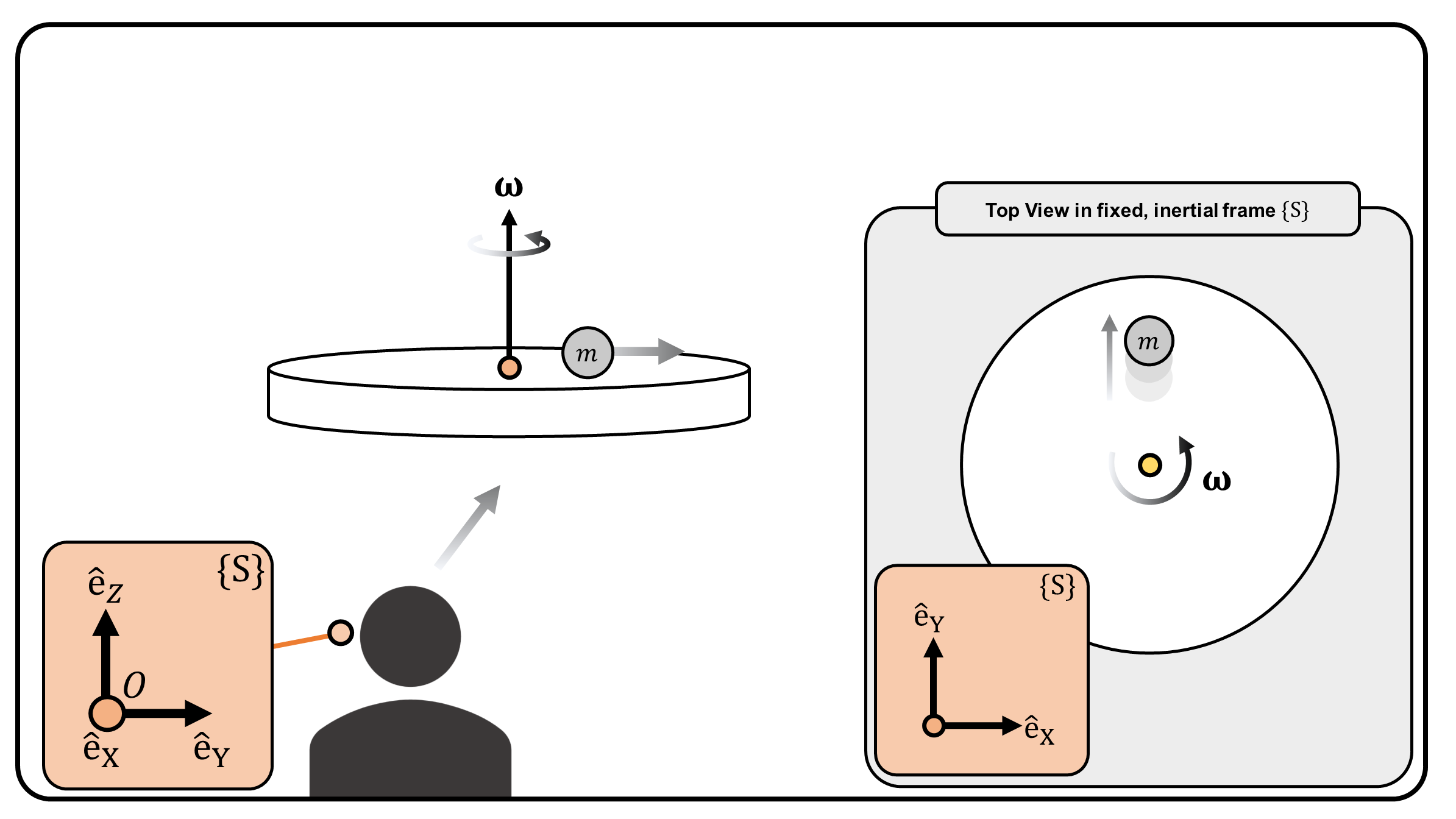
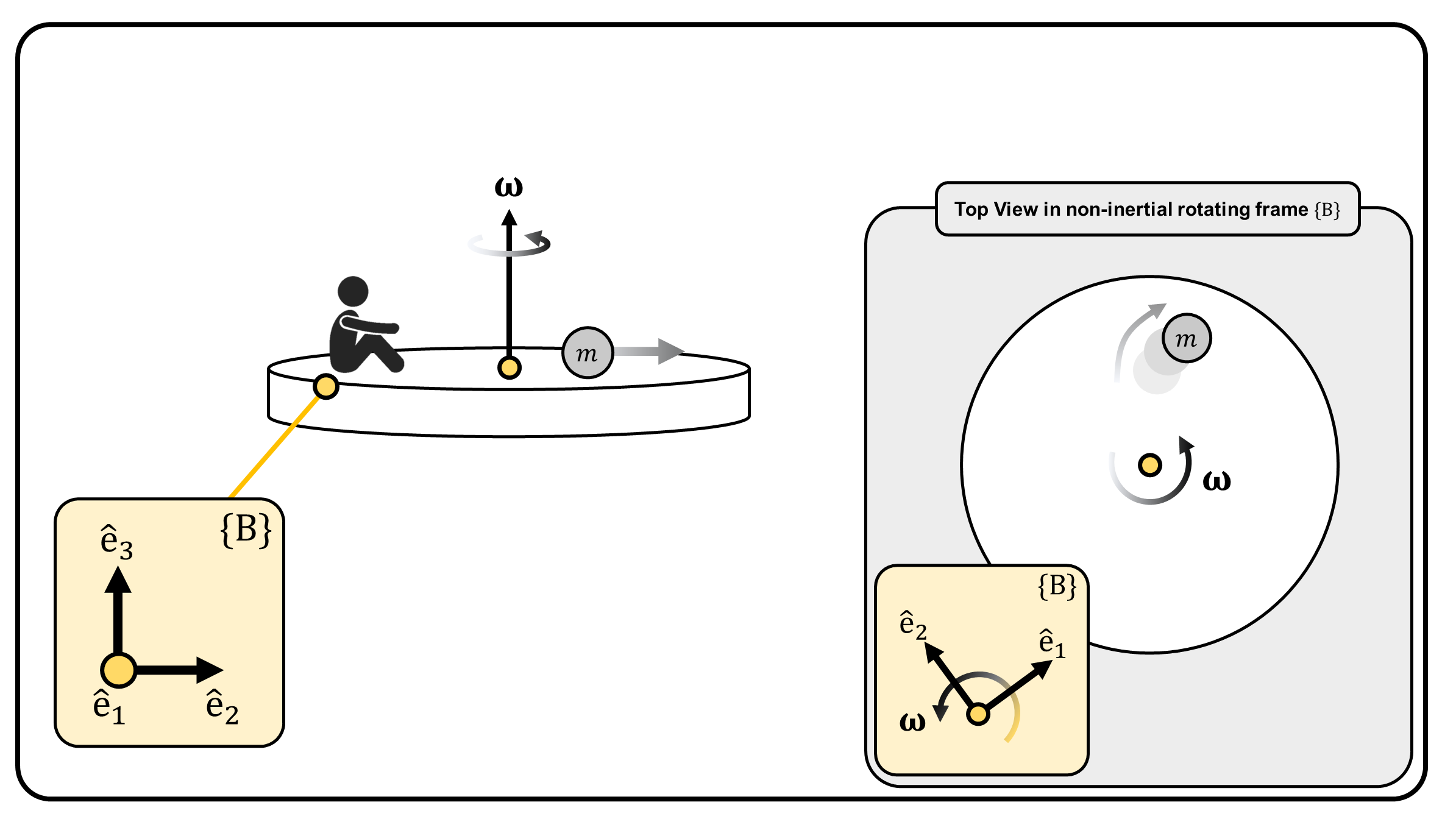
**(Figure 2)** **(Top)** A particle with mass $m$ sliding on a frictionless, rotating table, observed in frame $\{S\}$ which is a fixed, inertial reference frame. **(Bottom)** A particle with mass $m$ sliding on a frictionless, rotating table, observed in frame $\{B\}$ which is a non-inertial reference frame

(Figure 2) (Top) A particle with mass \(m\) sliding on a frictionless, rotating table, observed in frame \(\{S\}\) which is a fixed, inertial reference frame. (Bottom) A particle with mass \(m\) sliding on a frictionless, rotating table, observed in frame \(\{B\}\) which is a non-inertial reference frame


Summary

Summarizing, on a rotating frame there are three fictitious forces:

  • The Coriolis Force \(\mathbf{F}_{Coriolis}=- 2m \big( \boldsymbol{\omega}\times \mathbf{v}' \big)\). Cyclones and trade winds are examples of the impact of the Coriolis force. Moreover, Foucault’s celbrated experiment of the precessing pendulum. Note that the Coriolis force depends on the direction of angular velocity \(\boldsymbol{\omega}\). Hence, the Coriolis force experienced by the Northern and Southern hemisphere are opposite.

  • Euler Force \(\mathbf{F}_{Euler}= -m\big(\boldsymbol{\alpha}' \times \mathbf{r}\big)\). This fictitious force is observed for non-uniformly rotating reference frames, i.e., the angular velocity \(\boldsymbol{\omega}\) changes with respect to time.

  • Centrifugal Force \(\mathbf{F}_{centrifugal}=-m\big\{\boldsymbol{\omega} \times \big( \boldsymbol{\omega} \times \mathbf{r} \big) \big\}\). The centrifugal force is directed radially outwards from the rotating axis. We often experience this force when we ride on rollercoasters.



References

[1]
C. Lanczos, The variational principles of mechanics. Courier Corporation, 2012, p. 101.

  1. Inertia force is important when we discuss about d’Alembert’s principle.↩︎

  2. It is worth emphasizing that frame \(\{S\}\) and frame \(\{B\}\) are describing the same \(\mathbf{r}\), but the components with respect to the bases of frame \(\{S\}\) and frame \(\{B\}\) are different. As Prof. Schuller mentioned, we should not do chart-dependent physics. ↩︎