Newton’s Laws of Motion
Moses C. Nah
2023-03-06
Introduction
Nature and Nature’s laws lay hid in night.
God said, “Let Newton be!” and all was light.
Isaac Newton established the three physical laws of motion that laid the foundation of dynamics — one of the main branches of classical mechanics:
- First Law — In an inertial frame of reference, an object either remains at rest or continues to move at a constant speed in a straight line, unless acted upon by a force.1 2
- Second Law — In an inertial frame of reference, the sum of forces acting upon an object is the rate of change of momentum of a body.3
- Third Law — When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.
The beauty of dynamics is that all of the details stem from these three laws of motion stated by Newton.4
As our initial step to study classical mechanics, we focus on applying Newton’s laws of motion to an idealized single particle or a mass point, i.e., the size of the object is negligible. This enables us to neglect additional degrees of freedom like rotation or spin, which are important motions for objects with non-negligible size.
Momentum Principle for a Single Particle
Consider a point particle with mass \(m\). Newton’s Second Law states that: \[ \sum \mathbf{F} = \dot{\mathbf{p}} \tag{1} \] In this equation, \(\sum\mathbf{F}\in\mathbb{R}^3\) is the sum of forces applied to the mass particle (Figure 1); \(\mathbf{p}\in\mathbb{R}^3\) is the linear momentum of the particle, defined by \(\mathbf{p} :=m\mathbf{v}\); \(\mathbf{v}\in\mathbb{R}^3\) is the velocity vector of the particle.
Equation 1, which is Newton’s Second Law of motion, is often referred to as the linear momentum principle for a single particle.
Usually, point mass \(m\) is constant, and Equation 1 is reformulated as: \[ \mathbf{F} = \dot{\mathbf{p}} = m \dot{\mathbf{v}} = m\mathbf{a} \tag{2} \] In this equation, \(\mathbf{a}\in\mathbb{R}^3\) is the acceleration of the particle. This is the renowned force equals mass times acceleration equation.
. **(Right)** The sum of forces results in a single force vector: $\mathbf{F_{total}}:=\mathbf{\sum{F}}_i$.](images/dynamics_force_vector_add.png)
(Figure 1) (Left) A single particle with mass \(m\) applied by multiple forces. The force vectors are added using the parallelogram rule. (Right) The sum of forces results in a single force vector: \(\mathbf{F_{total}}:=\mathbf{\sum{F}}_i\).
Conservation of Linear Momentum
It is immediate from the linear momentum princiiple that if the total force applied to the particle is a zero vector, \(\sum\mathbf{F}=\mathbf{0}\), the linear momentum of the particle \(\mathbf{p}\) is conserved. This is the conservation of linear momentum: \[ \mathbf{F} = \mathbf{0} = \dot{\mathbf{p}} ~~ \Longrightarrow ~~ \mathbf{p} = \text{a constant vector} \] Conservation of linear momentum is embodied in Newton’s First Law of motion, which is also referred to as the law of inertia. But as mentioned in the second footnote, Newton’s First Law of motion is more than a special case of the Second Law of motion.
Remark — Vectorial Mechanics
It is worth emphasizing that Equation 1, Newton’s Second Law of motion, is a vector equation, i.e., a collection of equations. Under the choice of an inertial reference frame, there are 2 (3) differential equations for a motion 2D (3D) space.
As an example, consider Figure 2. Since the bases of a fixed, inertial frame \(\{S\}\), \(\mathrm{\hat{e}_X}\) and \(\mathrm{\hat{e}_Y}\) are linearly independent, each component of the basis must be equal: \[ F_x \mathrm{\hat{e}_{X}} + F_y \mathrm{\hat{e}_{Y}} = \frac{d}{dt}\big( p_x \mathrm{\hat{e}_X} + p_Y \mathrm{\hat{e}_Y} \big) = \dot{p}_x \mathrm{\hat{e}_X} + \dot{p}_Y \mathrm{\hat{e}_Y } ~~~~~~~~~~~ F_x = \dot{p}_x, ~~~ F_y = \dot{p}_y \] Note that \(\mathrm{\hat{e}_X}\) and \(\mathrm{\hat{e}_Y}\) consist the bases of a fixed, inertial frame, hence are excluded for the time differentiation.
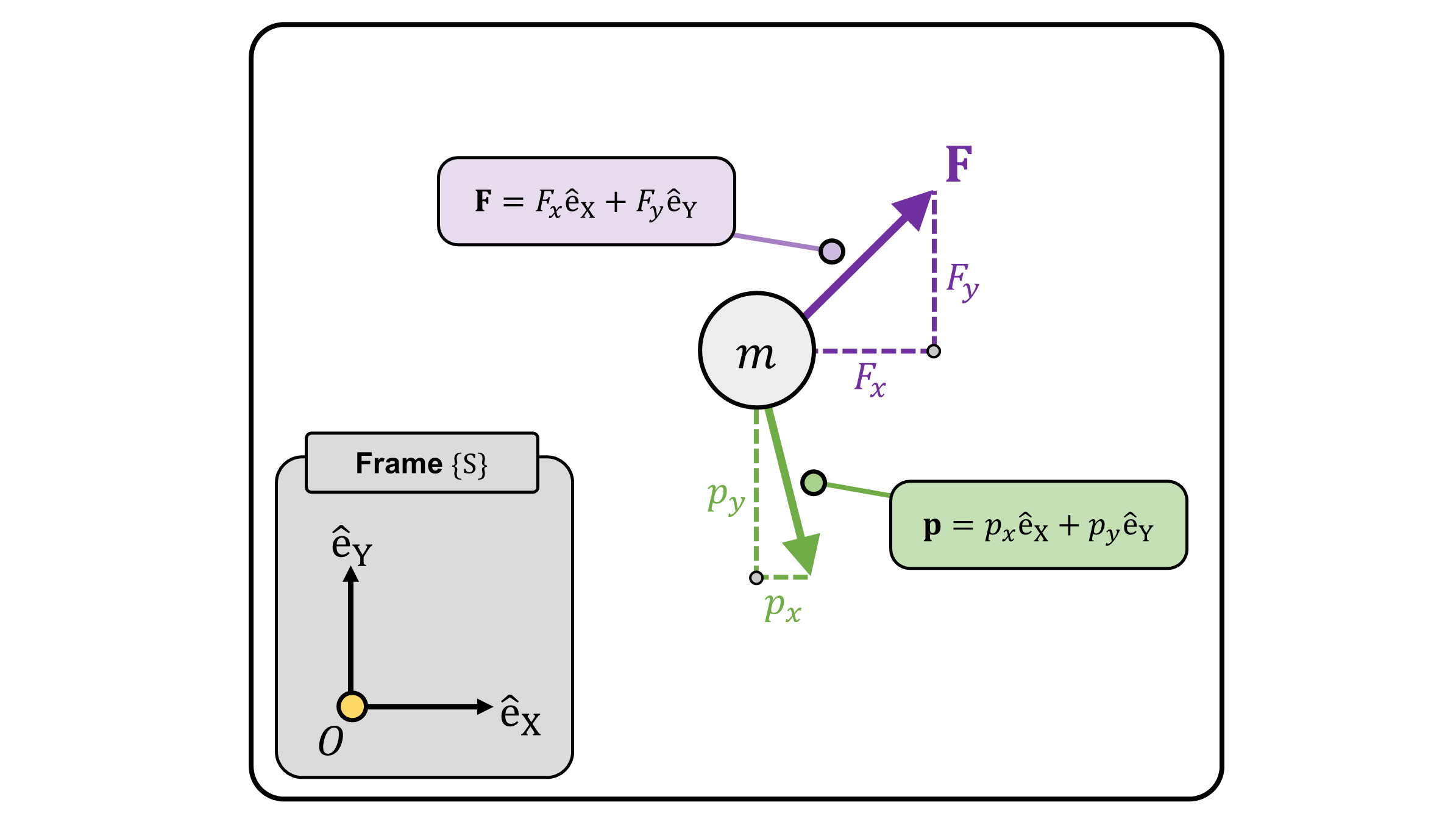
(Figure 2) Under an fixed, inertial frame \(\{S\}\) attached to the origin \(O\), Equation 1 is a collection of 2 differential equations.
Work – Energy Principle
Consider a single particle with mass \(m\) moving along trajectory \(\mathbf{r}(t)\) parameterized with time \(t\) (Figure 3). The particle is applied by a single force \(\mathbf{F}\).
Given two points \(\mathbf{r_1}:=\mathbf{r}(t_1)\) and \(\mathbf{r_2}:=\mathbf{r}(t_2)\) on trajectory \(\mathbf{r}(t)\), we define a physical quantity called mechanical work \(W\) done by force \(\mathbf{F}\) as: \[ W := \int_{\mathbf{r_1}}^{\mathbf{r_2}} \mathbf{F}\cdot d\mathbf{r} \] In this equation, \(\cdot\) is a dot product of two vectors.
Moreover, we define a physical quantity called kinetic energy \(T\) of the particle with mass \(m\) and velocity \(\mathbf{v}\) as: \[ T := \frac{1}{2}m\mathbf{v}\cdot \mathbf{v} = \frac{1}{2}m ||\mathbf{v}||^2 \] In this equation, for \(\mathbf{v}\in\mathbb{R}^n\), \(||\mathbf{v}||^2:=\sum_{i=1}^n v_i^2\).
Based on the definitions of mechanical work \(W\) and kinetic energy \(T\), we derive the work-energy principle. Using the linear momentum principle of the particle: \[ \begin{align*} W &:= \int_{\mathbf{r_1}}^{\mathbf{r_2}}\mathbf{F} \cdot d\mathbf{r}= \int_{\mathbf{r_1}}^{\mathbf{r_2}} m \dot{\mathbf{v}} \cdot d\mathbf{r} \\ &= \int_{\mathbf{v_1}}^{\mathbf{v_2}} m\mathbf{v} \cdot d\mathbf{v} = \frac{1}{2}m ||\mathbf{v_2}||^2 - \frac{1}{2} m||\mathbf{v_1}||^2 := T_2 - T_1 \tag{3} \end{align*} \] In these equations, \(T_1\) and \(T_2\) are the kinetic energy of the mass with velocity \(\mathbf{v_1}\), \(\mathbf{v_2}\), respectively.5
The work-energy principle states that the mechanical work done by a single force \(\mathbf{F}\) from point \(\mathbf{r_1}:=\mathbf{r}(t_1)\) to \(\mathbf{r_2}:=\mathbf{r}(t_2)\), is simply the difference of kinetic energy between the two points, \(T_2 - T_1\).
It is immediate that for multiple forces applied to the particle, we consider the total mechanical work \(W_{total}\) which consists of work done by each force: \[ W_{total} = \sum_{i} W_i = \sum_{i}\int_{\mathbf{r_1}}^{\mathbf{r_2}}\mathbf{F}_i\cdot d\mathbf{r} = \int_{\mathbf{r_1}}^{\mathbf{r_2}}\big(\sum_{i}\mathbf{F}_i\big)\cdot d\mathbf{r}= \int_{\mathbf{r_1}}^{\mathbf{r_2}} m \dot{\mathbf{v}} \cdot d\mathbf{r} = T_2-T_1 \]
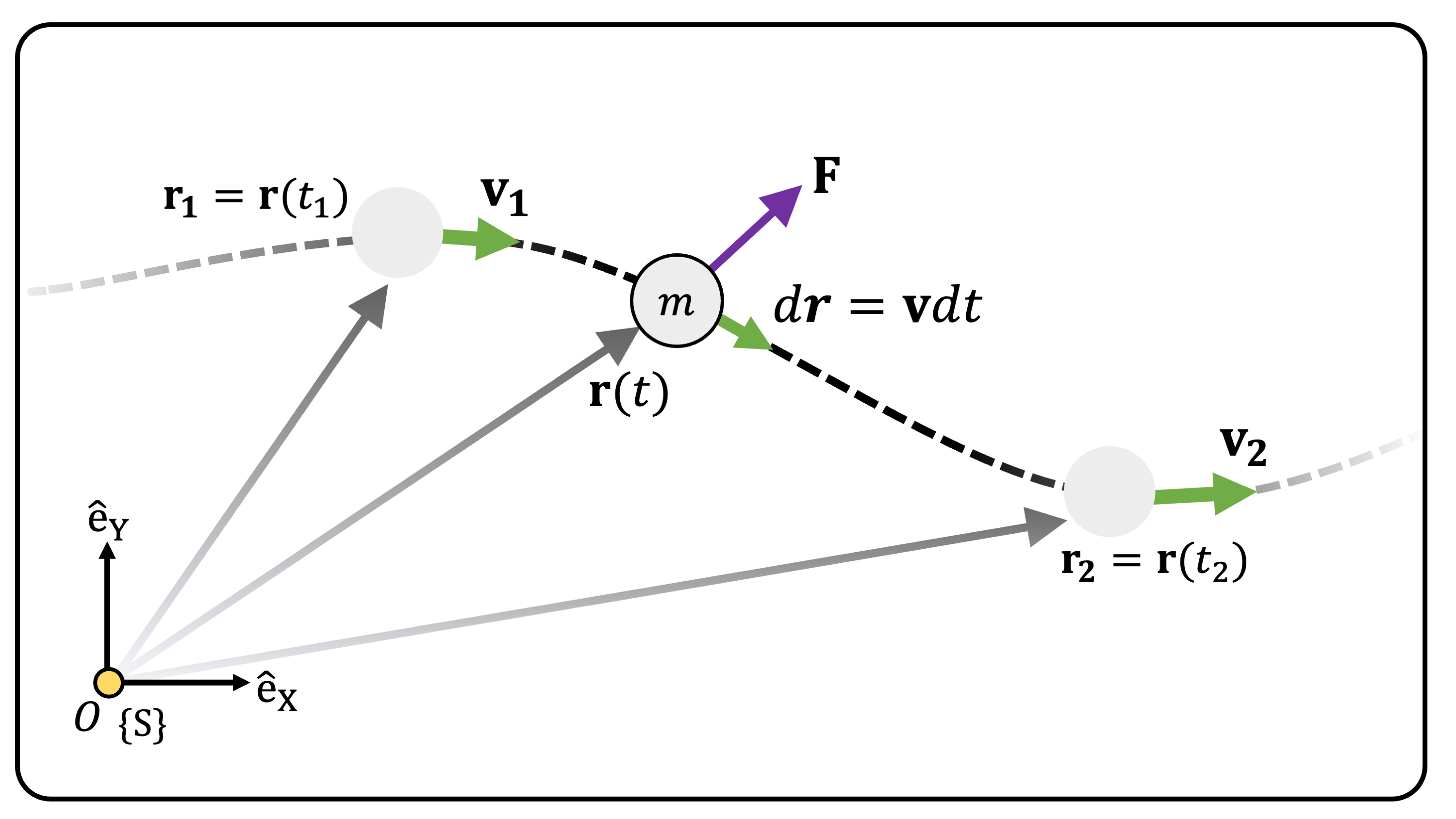
(Figure 3) A particle with mass \(m\) moving along trajectory \(\mathbf{r}(t)\) under the influence of force \(\mathbf{F}\)
Conservation of Energy
If force \(\mathbf{F}\) is a conservative force [refer to this post], i.e., if force \(\mathbf{F}\) can be described as a gradient of a potential function \(U(\mathbf{r})\), \(\mathbf{F}(\mathbf{r})=- \nabla U(\mathbf{r} )\), Equation 3 is reformulated as: \[ \begin{align*} T_2 - T_1 &= \int_{\mathbf{r_1}}^{\mathbf{r_2}}\mathbf{F} \cdot d\mathbf{r} = \int_{\mathbf{r_1}}^{\mathbf{r_2}} - \nabla U(\mathbf{r} ) \cdot d\mathbf{r}\\ &=\int_{U(\mathbf{r_1})}^{U(\mathbf{r_2})} -dU = U(\mathbf{r_1}) - U(\mathbf{r_2}) := U_1 - U_2 \end{align*} \] We derived the law of conservation of energy: \[ T_1 + U_1 = T_2 + U_2 \tag{4} \] In other words, for a particle under the influence of a conservative force field, the sum of kinetic and potential energy is conserved.
[Example 1] Free Fall of a Particle
Consider a particle with mass \(m\) located at height \(h_0\) at rest (Figure 4). The particle is sufficiently near the Earth’s surface, hence we assume uniform gravitational force. Our goal is to analyze the motion of the particle as a function of time.
Since the particle is near the Earth’s surface, the gravitational force experienced by the particle is \(-mg\mathrm{\hat{e}_Y}\). The linear momentum principle along axis \(\mathrm{\hat{e}_Y}\) provides the second-order differential equation which governs the motion of the particle: \[ m\ddot{h} = -mg \] In this equation, \(h(t)\) is the height of the object at time \(t\) measured from the ground; \(g\) is the gravitational acceleration, which is \(g=9.81m/s^2\).
The problem is now reduced to the integration of the differential equation, given the initial condition \(h(0)=h_0\) and \(\dot{h}(0)=0\): \[ \dot{h}(t) := v(t) = -gt, ~~~~~~ h(t) = h_0-\frac{1}{2}gt^2 \] From these equations, we can derive the time \(T\) it takes for the particle to reach the ground (i.e., \(h=0\)), and also the velocity \(v(h)\) as a function of \(h\): \[ T = \sqrt{\frac{2h_0}{g}}, ~~~~ v(h)= \sqrt{2g(h_0-h)} \] Note that \(T\) and \(v(h)\) is not a function of \(m\).
These results shows that no matter how light or heavy the object is, if the object is dropped at the same height, they all reach the same velocity when it hits the ground. Moreover, all objects arrive at the same time. This equation is consistent with the famous Galileo’s legendary experiment conducted on the Tower of Pisa.
Since gravity is a conservative force, the law of conservation of energy can also be used to derive the results. The potential energy \(U(h)\) is defined by \(U(h)=mgh\). Since the particle is dropped at rest at height \(h_0\), using the law of conservation of energy, we can derive the velocity of the object at arbitrary height \(h<h_0\): \[ mgh_0 + 0 = mgh + \frac{1}{2}mv^2, \;\;\;\; v= \sqrt{2g(h_0-h)} \] The time it takes for the object to reach the ground (i.e., \(h=0\)) can be derived by integration: \[ v = \frac{dh}{dt}= \sqrt{2g(h_0-h)}, \;\;\;\;\; \int_{h_0}^{0} \frac{dh'}{\sqrt{2g(h_0-h')}} = \int_{0}^{T}dt, \;\;\; T = \sqrt{\frac{2h_0}{g}} \]
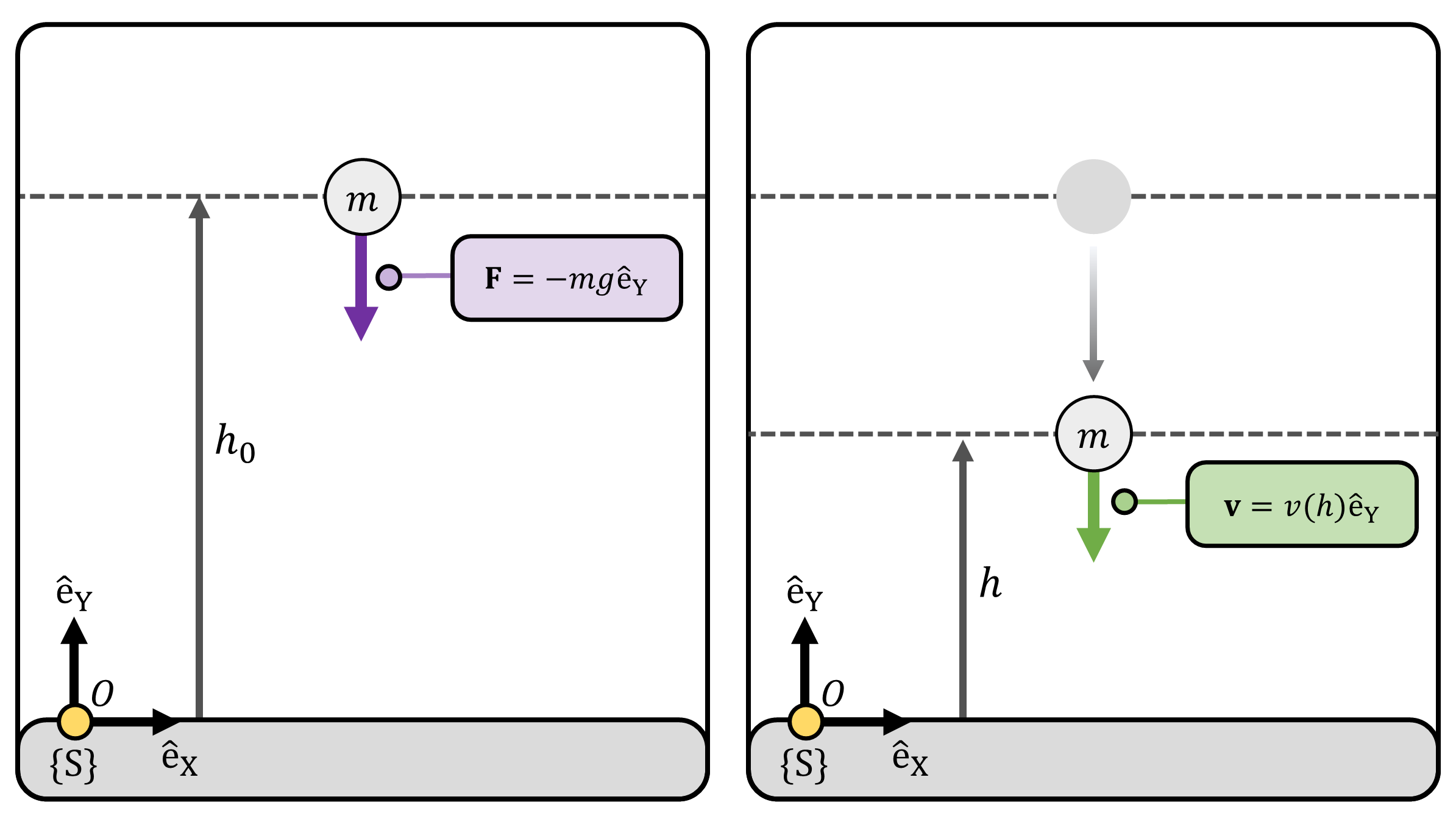
(Figure 4) (Left) A particle with mass \(m\) at height \(h_0\) at rest. The gravitational force experienced by the object is \(-mg\mathrm{\hat{e}_Y}\). (Right) The velocity \(v(h)\) of the particle at height \(h\).
[Example 2] Particle Sliding Down an Arbitrary Curve [2]
Consider a particle with mass \(m\) sliding down an arbitrary curve (Figure 5). Assume no friction on the surface of the curve.
From height \(h_0\) to \(h_1\), the work done by gravity is: \[ \begin{align*} dW &= \mathbf{F}\cdot d\mathbf{s} = -mg \sin \theta ds = -mg \frac{dh}{ds} ds = -mg dh \\ W &= \int_{h_0}^{h_1}-mg dh = mg (h_0-h_1) \end{align*} \] The result shows that mechanical work \(W\) done by gravity does not depend on the shape of the curve, but only depends on the height difference \(h_0 -h_1\). Note that this result is identical to the free fall case.
To use the work–energy principle, we also need to account for the work done by the normal force which the surface of the curve exerts. However, normal force is a constraint force, which is always orthogonal to the velocity of the object.6 Therefore, the work done by the normal force is zero: \[ mg(h_0-h_1) = \frac{1}{2}mv^2 ~~~~~~~~~~~ v_1 = \sqrt{2g(h_0-h_1)} \] The result of this simple example is quite astonishing: No matter what the shape of the curve is, if the particles start at the same height at rest, the resulting velocities are all identical (Figure 5) (Right).
As shown in Example 1, we can also use the law of conservation of energy to derive this result. Again for this case, the presence of normal force can be ignored.
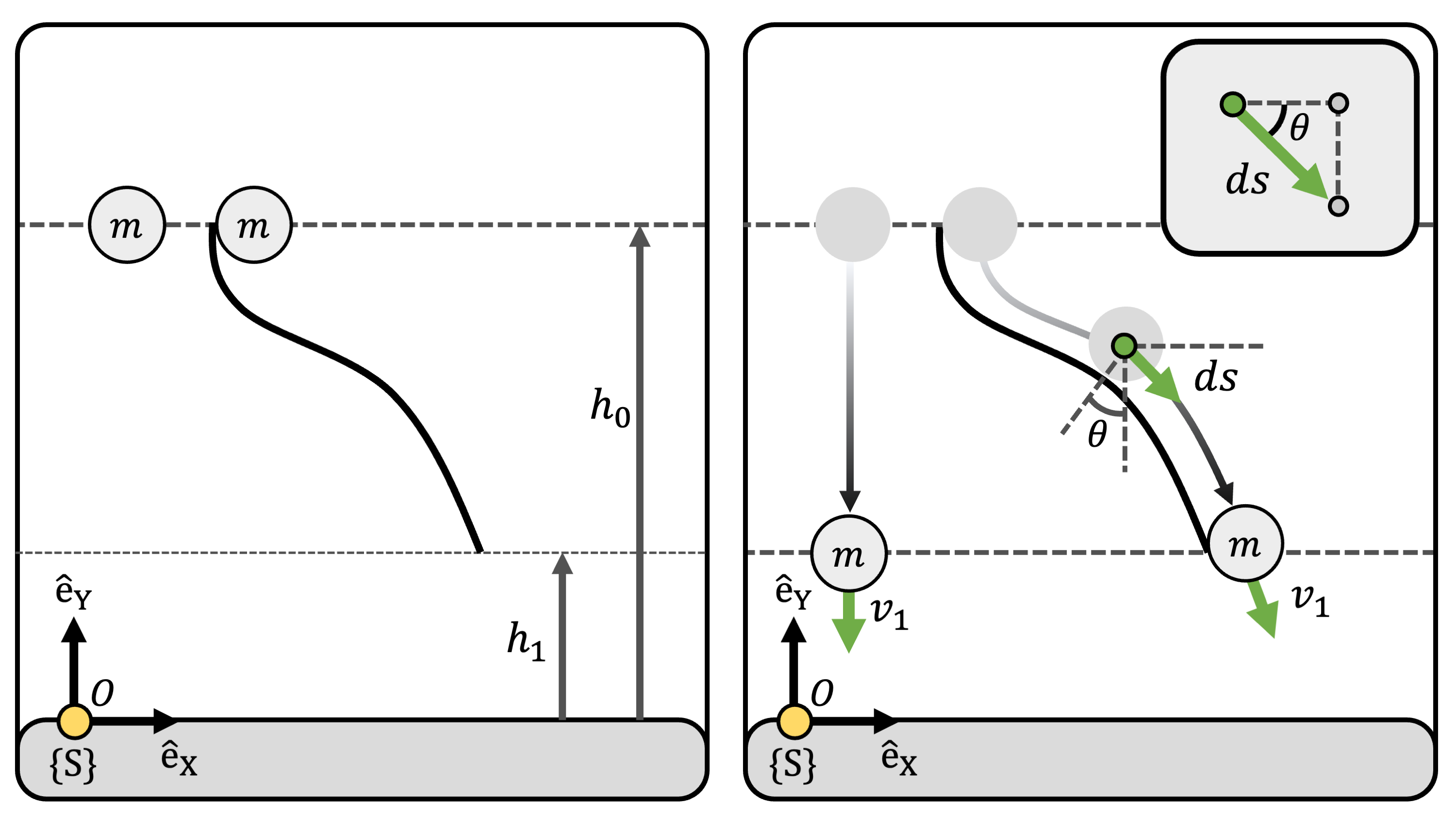
(Figure 5) (Left) A particle with mass \(m\) under the influence of gravity \(mg\) sliding down an arbitrary curve. (Right) No matter what the shapes of the curve are, the resulting velocities \(v\) at height \(h_1\) are all identical
References
Inertial (or Galilean) frame of reference is a frame of reference which is at rest or which is moving at a constant speed in a straight line. In other words, it is a frame of reference that is neither accelerating nor decelerating. Throughout this post, we often define an inertial frame of reference, usually a frame that is fixed at the origin, and then describe the object’s motion with respect to that frame. ↩︎
The author is aware about the modern view of Newton’s laws of motion, where an inertial frame of reference which is an absolute frame of reference is not needed. For details, please refer to this video from Prof. Schuller. In fact, adding an observer at absolute rest seems artificial, placing the inertial observer privileged over others. However, a detailed discussion about this is outside the scope of our post, and we introduce an inertial observer that is at absolute rest. ↩︎
At this point, one might be confused and think that the first law is redundant, since it is a special case of the second law (i.e., a special case when sum of forces is zero). As Prof. Schuller said, Newton wasn’t naïve. The first law is used as a measurement prescription of what a straight line is. Again, I highly recommend watching this part of the video from Prof. Schuller.↩︎
The two main branches of classical mechanics are Vectorial mechanics and Analytical mechanics [1]. Newton’s Laws of motion is categorized as Vectorial mechanics, since the main goal is to identify the vector quantities such as forces and linear momentum to derive the second-order differential equation. The discussion of analytical mechanics is made on later posts. ↩︎
A small mathematical trick is used, where \(\dot{\mathbf{v}}\cdot d\mathbf{r}=\dot{\mathbf{v}}\cdot\mathbf{v}dt = \mathbf{v} \cdot d\mathbf{v}\).↩︎
In fact, this is related to the principle of virtual work, which we discuss in a later post.↩︎