Angular Momentum Principle of Rigid Object

Introduction

As we discussed about the center of mass and moment of inertia of a rigid object, we are now ready to discuss in detail about Euler’s second law of motion, i.e., the angular momentum principle of rigid object: \[ \sum \boldsymbol{\tau}_{ext,A} = \frac{d\mathbf{H}_A}{dt} \] Recall that \(\boldsymbol{\tau}_{ext,A}\), \(\mathbf{H}_A\) are the external torque and angular momentum about point \(A\), respectively. As before, in this post we consider a system with \(N\) particles (Figure 1). The equations are immediately generalized to the case of continuous distribution of masses.

(Figure 1) A rigid object consisting of \(N\) mass particles. (Right) A simplified depiction of rigid object on left.

Angular Momentum about the Center of Mass

Consider point \(A\) that is fixed in space.

Angular Momentum, relation between two Points

Consider two points, point \(A\) and \(B\) fixed in space. Let the angular momentum about point \(A\) and \(B\) be \(\mathbf{H}_A\), \(\mathbf{H}_B\). By definition, the angular momentum about point \(A\) \((B)\) is the sum of the angular momentum of \(N\) particles, with respect to the distance measured from point \(A\) \((B)\) (Figure 2): \[ \mathbf{H}_A =\sum_{i=1}^{N} \mathbf{r}_i \times m_i\mathbf{v}_i ~~~~~~~~~~~~~~~~~ \mathbf{H}_B =\sum_{i=1}^{N} \mathbf{r}_i' \times m_i\mathbf{v}_i \] Using the kinematic relation \(\mathbf{r}_i = \mathbf{r}+\mathbf{r}_i'\): (Figure 2, Right) \[ \mathbf{H}_A = \sum_{i=1}^{N} \mathbf{r}_i \times m_i\mathbf{v}_i = \sum_{i=1}^{N} (\mathbf{r}+\mathbf{r}_i') \times m_i\mathbf{v}_i = \mathbf{r}\times \sum_{i=1}^{N}m_i\mathbf{v}_i + \underbrace{\sum_{i=1}^{N} \mathbf{r}_i' \times m_i\mathbf{v}_i}_{:=\mathbf{H}_B} = \mathbf{r}\times \sum_{i=1}^{N}m_i\mathbf{v}_i + \mathbf{H}_B \] To further simplify the equation, we use the definition of the center of mass of the rigid object. Let the center of mass of the object be \(\mathbf{R}\). By definition: \[ \mathbf{R} := \frac{1}{M}\sum_{i=1}^{N}m_i\mathbf{r}_i ~~~~~~~~~ \mathbf{V} :=\frac{d\mathbf{R}}{dt} = \frac{1}{M}\sum_{i=1}^{N}m_i\mathbf{v}_i \] In these equations, \(M:=\sum m_i\) is the total mass of the rigid object.

The relation between \(\mathbf{H}_A\), \(\mathbf{H}_B\) is: \[ \mathbf{H}_A = \mathbf{H}_B + \mathbf{r}\times M\mathbf{V} := \mathbf{H}_B + \mathbf{r}\times \mathbf{P} \tag{1} \] In this equation, \(\mathbf{P}\) is the total linear momentum of the rigid object.

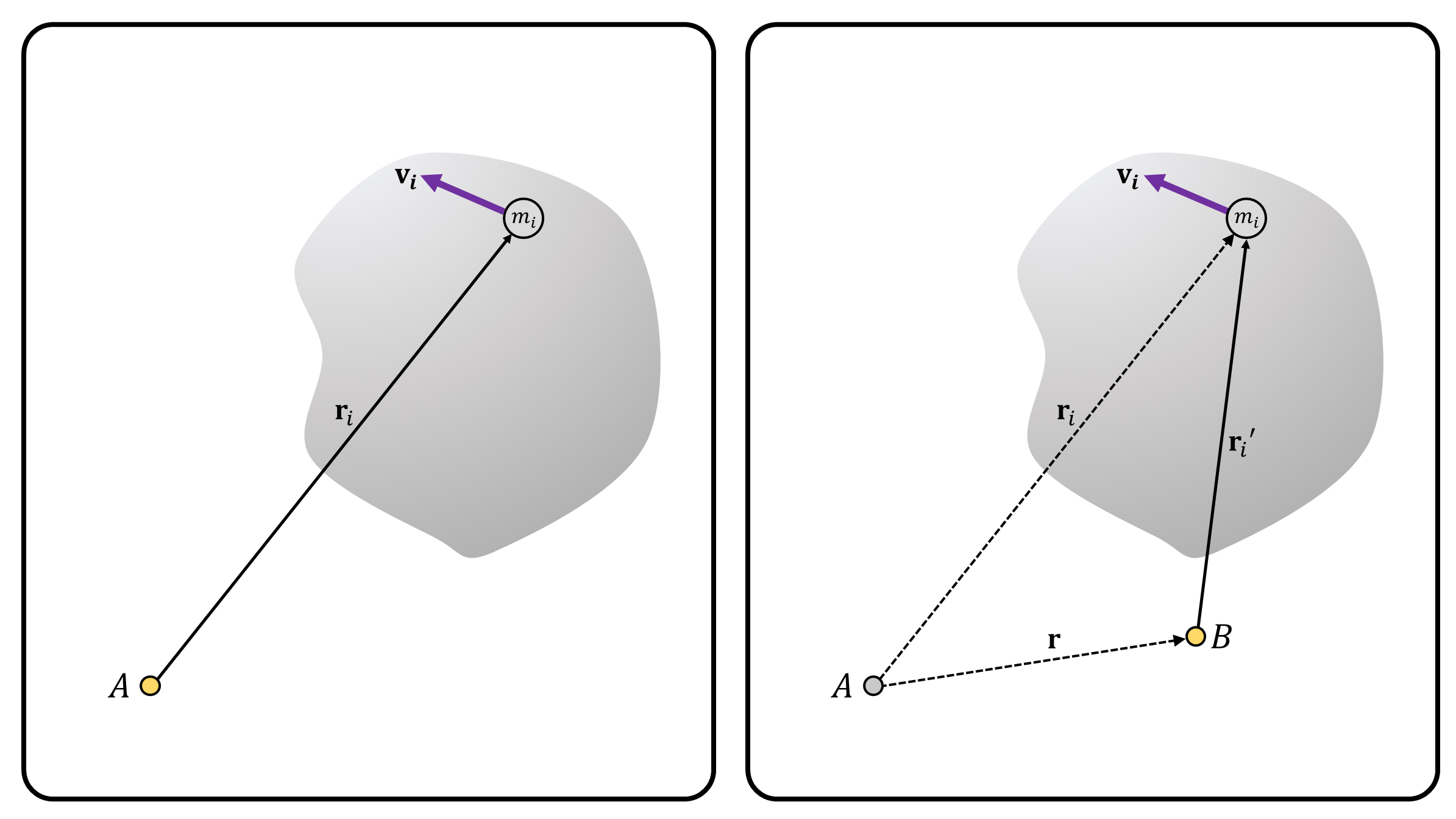
(Figure 2) (Left) Angular momentum of the rigid object about point \(A\). (Right) Angular momentum of the rigid object about point \(B\). The kinematic relation between \(A\), \(B\) and the \(i\)-th particle.

Angular Momentum, Center of Mass

While Equation 1 is straightforward to derive, it is quite hard to extract out the physical meaning lurking under the equation. But if we pick point \(B\) to be the center of mass of the rigid object (which we refer to as point \(C\)), we can

Summary

References