Introduction
In this post, we discuss about Denavit-Hartenberg
(DH) parameters. DH parameters is one of the popular methods for
analyzing the Forward Kinematics of a robotic manipulator. There are
three main DH parameter conventions [1],
including the original notation suggested by Denavit and Hartenberg
[2], [3].
Here, we introduce the modified (or) DH parameters [1].
Denavit-Hartenberg (DH) Convention
Consider an \(n\)-DOF open-chain
robotic manipulator which consists of \(n\) rigid links. We define two reference
frames — frame \(\{S\}\) fixed to the
ground and frame \(\{B\}\) attached to
the end-effector of the \(n\)-th link.
robot. For this section, we simply substitute frame \(\{S\}\) to frame \(\{0\}\).
Given the \(n\) generalized
coordinates of the robotic manipulator \(\mathbf{q}=(q_1, q_2, \cdots,
q_n)\in\mathbb{R}^{n}\), the goal is to find the orientation and
position of the end-effector. In other words, we aim at finding the
Forward Kinematics map of the robotic manipulator \({}^{0}\mathbf{H}_{B}(\mathbf{q}) \in
SE(3)\) as a function of the generalized coordinates of the
robotic manipulator.
One can derive the Forward Kinematics map by defining a sequence of
\(n\) reference frames to the \(n\) joints of the robot, and define the
relation between the adjacent frames: \[
{}^{0}\mathbf{H}_{B}(\mathbf{q}) = {}^{0}\mathbf{H}_{1}(q_1)
{}^{1}\mathbf{H}_{2}(q_2) \cdots {}^{n-1}\mathbf{H}_{n}(q_n)
{}^{n}\mathbf{H}_{B}
\] In this equation, frame \(\{i\}\) for \(i=0,1,\cdots, n\) is attached to the \(i\)-th link of the robot. For \(i=0\), we consider the fixed ground as the
\(0\)-th link (i.e., base frame) of the
robot. Moreover, \({}^{n}\mathbf{H}_{B}\in
SE(3)\) since frame \(\{n\}\)
and frame \(\{B\}\) are both attached
to the \(n\)-th link.
Rather than defining these reference frames in an arbitrary fashion,
DH convention is a set of rules for placing this
sequence of reference frames.
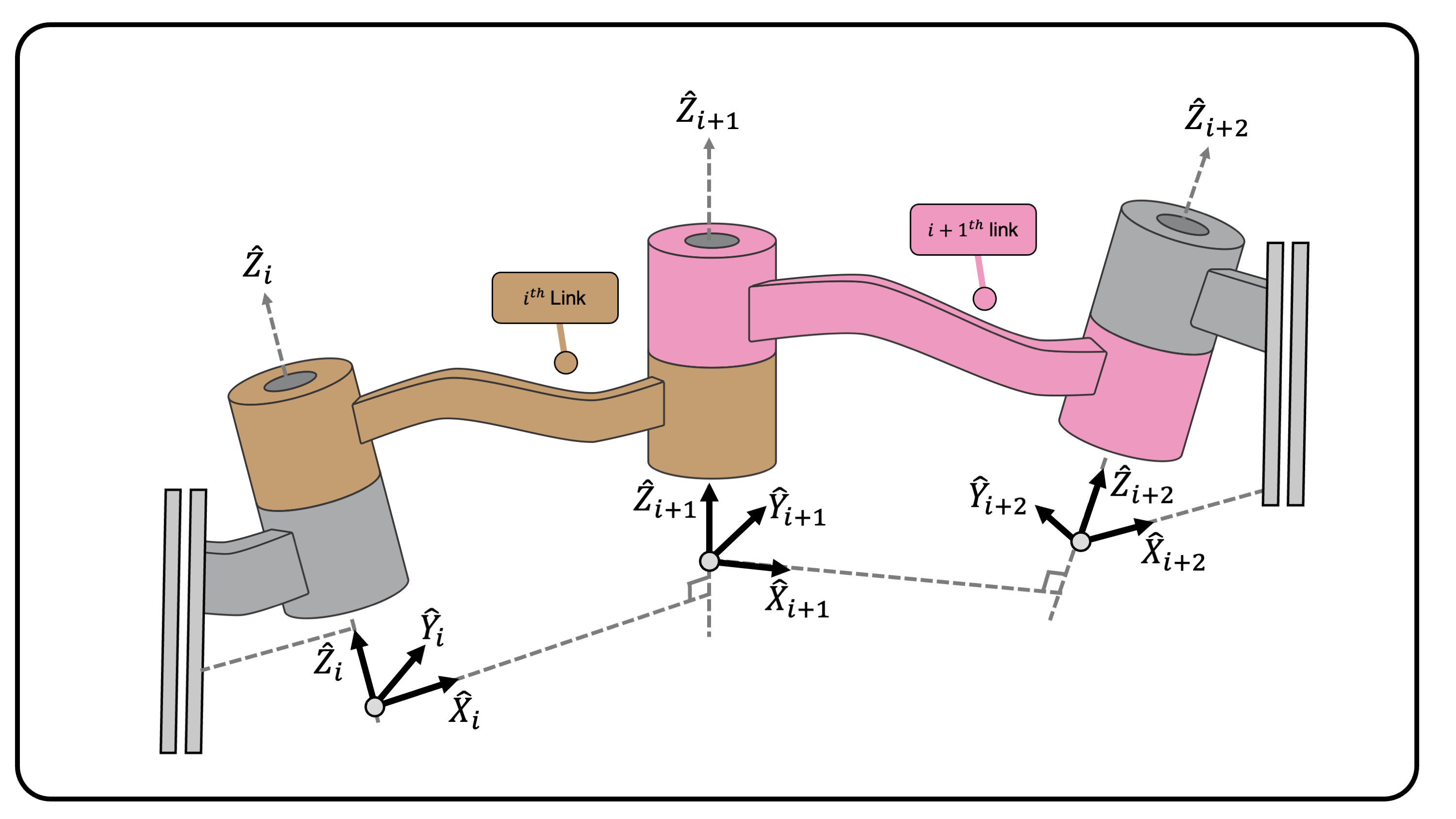
Defining the Reference Frames
Given frame \(\{B\}\) attached at
the end-effector of the robot, one has to define \(n+1\) reference frames — frame \(\{0\}\) to frame \(\{n\}\). Each reference frame consists of
three mutually orthonormal bases. We denote the bases of frame \(\{i\}\) as \(\hat{X}_i, \hat{Y}_i, \hat{Z}_i\).
DH convention provides a set of rules to define \(\hat{X}_i, \hat{Y}_i, \hat{Z}_i\) for \(i = 0,1,\cdots, n\).
- (Step 1) For \(i= 1, 2,
\cdots, n\), attach \(\hat{Z}_i\) along the \(i\)-th joint. If the \(i\)-th joint is a revolute joint, \(\hat{Z}_i\) coincides with the axis of
rotation. If the \(i\)-th joint is a
prismatic joint, \(\hat{Z}_i\)
coincides with the axis of translation.
- (Step 2) Given \(\hat{Z}_1, \hat{Z}_2, \cdots, \hat{Z}_n\)
from step 1, consider a pair of adjacent axes \(\hat{Z}_{i}\) and \(\hat{Z}_{i+1}\) for \(i=1,2,\cdots,n-1\). Find a line segment
which is mutually orthogonal to the adjacent joint axes \(\hat{Z}_i\) and \(\hat{Z}_{i+1}\). For \(i=1,2,\cdots,n-1\), the origin of the \(i\)-th frame is the point where the
perpendicular line segment intersects with \(\hat{Z}_{i}\).
- (Step 3) For \(i=1,2,\cdots,n-1\), the \(\hat{X}_{i}\) axis is along the
perpendicular line segment defined in step 2, directed from the \(i\)-th joint to the \(i+1\)-th joint.
- (Step 4) For \(i=1,2,\cdots,n-1\), the \(\hat{Y}_{i}\) axis is immediately defined
using the right-hand rule. At this moment frame \(\{1\}\), \(\{2\}\), , \(\{n-1\}\) are fully defined.
- (Step 5) Frame \(\{0\}\) is defined using frame \(\{1\}\). Axes \(\hat{X}_n, \hat{Y}_n\) of frame \(\{n\}\) are defined using frame \(\{n-1\}\).
Details of step 5 are deferred to the later section of this post.
Managing Exceptions
For step 2, there are two cases where the line segment which
intersects the adjacent joints (1) does not exists or (2) is not unique.
In detail, for \(i=1,2,\cdots,
n-1\):
- When adjacent joint axes \(\hat{Z}_i\) and \(\hat{Z}_{i+1}\) intersect, then there is no
line segment that is mutually orthogonal to both axes. For this case,
\(\hat{X}_i\) is defined to be the
cross product of \(\hat{Z}_i\) and
\(\hat{Z}_{i+1}\), i.e., \(\hat{X}_i:=\hat{Z}_i\times
\hat{Z}_{i+1}\).
- When adjacent joint axes \(\hat{Z}_i\) and \(\hat{Z}_{i+1}\) are parallel, there are
infinite many line segments that is mutually orthogonal to both axes.
For this case, we simply choose one line segment that is most
convenient.
The meaning of convenient is clarified in the next
section.
The Four DH Parameters
The DH convention enables us to define (1) the reference frames and
(2) the four parameters to define \({}^{i-1}\mathbf{H}_i(q_i),~~ i=1,2,\cdots
n\). First, the reference frames are defined as follows.