Given a small initial velocity \(v_0\), a disk of mass \(m\) and radius \(r\) begins rolling without slipping under the influence of gravity, \(g\), on a cylindrical surface of radius \(R\), as illustrated below. The frictional coefficient between the disk and the cylinder is \(\mu\). We are interested whether the disk detach from the cylindrical surface.

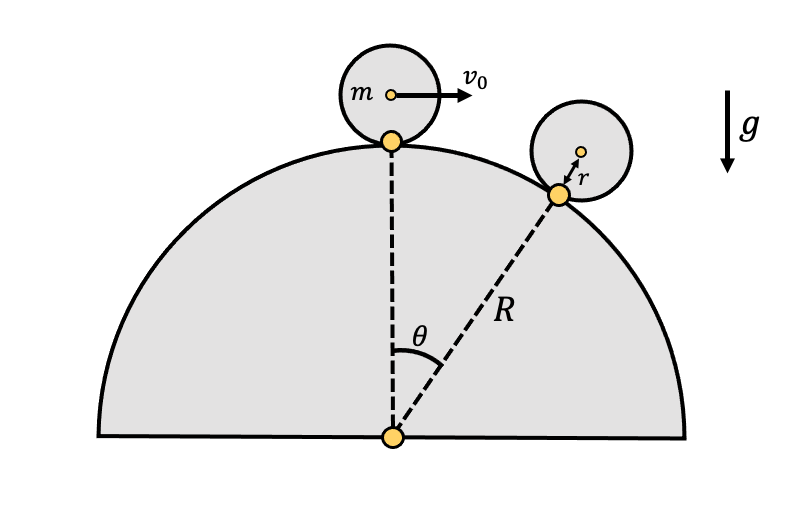
If we denote the angle rotated about the axis as \(\theta\), the equation of motion of this system is \(\tau = I \ddot{q}\). Using the work-energy principle, the equation is further expanded as follows: